In this self-paced course, we will continue using the subset of the Freddie Mac Single-Family dataset to try to predict the interest rate for a loan using H2O's XGBoost and Deep Learning models. We will explore how to use these models for a regression problem, and we will also demonstrate how to use H2O's grid search to tune the hyper-parameters of both models.
- Completion of the following self-paced course: Introduction to Machine Learning with H2O-3 - Classification.
- Some basic knowledge of machine learning.
- Familiarity with Python or R.
- An Aquarium account. If you do not have an Aquarium account, please refer to Appendix A of Introduction to Machine Learning with H2O-3 - Classification
Note: We recommend that you follow along on Aquarium, our cloud instance, to get similar results to the ones shown in this self-paced course. We also recommend that you go over the concepts section in Task 2 before starting your lab; that way, your instance is not running while you are going over the concepts. You can also use your personal machine with H2O-3, but keep in mind that you will see different results, as the machines have different results.
The data set we're using comes from Freddie Mac and contains 20 years of mortgage history for each loan and contains information about "loan-level credit performance data on a portion of fully amortizing fixed-rate mortgages that Freddie Mac bought between 1999 to 2017. Features include demographic factors, monthly loan performance, credit performance including property disposition, voluntary prepayments, MI Recoveries, non-MI recoveries, expenses, current deferred UPB, and due date of last paid installment." [1]
We're going to use machine learning with H2O-3 to predict the interest rate for each loan. To do this, we will build two regression models: an XGBoost model and a Deep Learning model that will help us find the interest rate that a loan should be assigned. Complete this self-paced course to see how we achieved those results.
We will start by importing H2O, the estimators for the algorithms that we will use, and the function to perform grid search.
#Import H2O and other libaries that will be used in this self-paced course
import h2o
from h2o.estimators import *
from h2o.grid import *
We now have to initialize our instance. If you are on Aquarium, it will connect to a local instance; if you are on your own machine, it will launch an instance connected to your machine.
import os
startup = '/home/h2o/bin/aquarium_startup'
shutdown = '/home/h2o/bin/aquarium_stop'
if os.path.exists(startup):
os.system(startup)
local_url = 'http://localhost:54321/h2o'
aquarium = True
else:
local_url = 'http://localhost:54321'
aquarium = False
h2o.init(url = local_url)
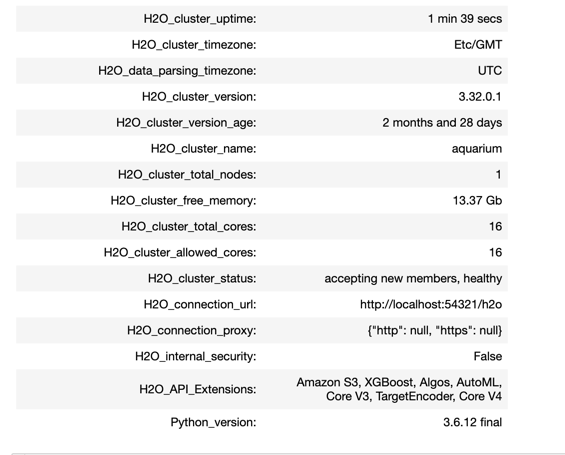
After initializing the H2O cluster, you will see the information shown above. We have an H2O cluster with just one node. If you are working on your machine, click on the link above the cluster information, and it will take you to your Flow instance where you can see your models, data frames, plots, and much more. If you are working on Aquarium, go to your lab and click on the Flow URL, and it will take you to a window similar to the one below. Keep it open on a separate tab, as we will come back to it later on.
Next, we will import the dataset. Since we are working with an S3 file, just specify the path of where the file is located, as shown below:
#Import the dataset
loan_level = h2o.import_file("https://s3.amazonaws.com/data.h2o.ai/DAI-Tutorials/loan_level_500k.csv")
Now that we have our dataset, we will explore some concepts and then do some exploration of the data and prepare it for modeling.
References
[1] Our dataset is a subset of the Freddie Mac Single-Family Loan-Level Dataset. It contains about 500,000 rows and is about 80 MB.
The data set we're using comes from Freddie Mac and contains 20 years of mortgage history for each loan and contains information about "loan-level credit performance data on a portion of fully amortizing fixed-rate mortgages that Freddie Mac bought between 1999 to 2017. Features include demographic factors, monthly loan performance, credit performance including property disposition, voluntary prepayments, MI Recoveries, non-MI recoveries, expenses, current deferred UPB, and due date of last paid installment." [1]
We're going to use machine learning with H2O-3 to predict the interest rate for each loan. To do this, we will build two regression models: an XGBoost model and a Deep Learning model that will help us find the interest rate that a loan should be assigned. Complete this self-paced course to see how we achieved those results.
We will start by importing H2O, the estimators for the algorithms that we will use, and the function to perform grid search.
# Import the H2O library
library(h2o)
We now have to initialize our instance. If you are on Aquarium, it will connect to a local instance; if you are on your own machine, it will launch an instance connected to your machine.
# Initialize the H2O Cluster
h2o.init(bind_to_localhost = FALSE, context_path = "h2o")
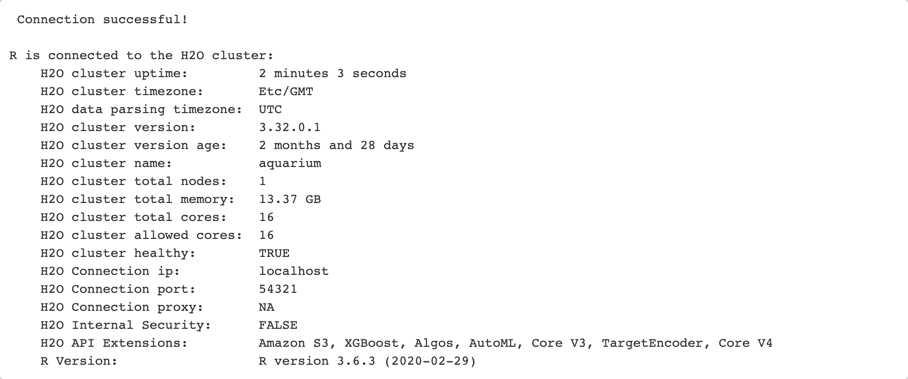
After initializing the H2O cluster, you will see the information shown above. We have an H2O cluster with just one node. If you are working on your machine, click on the link above the cluster information, and it will take you to your Flow instance where you can see your models, data frames, plots, and much more. If you are working on Aquarium, go to your lab and click on the Flow URL, and it will take you to a window similar to the one below. Keep it open on a separate tab, as we will come back to it later on.

Before we continue, we need to turn off the progress bar for readability purposes:
# Turn off progress bars for notebook readability
h2o.no_progress()
Next, we will import the dataset. Since we are working with an S3 file, just specify the path of where the file is located, as shown below:
# Import dataset
loan_level <- h2o.importFile(path = "https://s3.amazonaws.com/data.h2o.ai/DAI-Tutorials/loan_level_500k.csv")
Now that we have our dataset, we will explore some concepts and then do some exploration of the data and prepare it for modeling.
References
[1] Our dataset is a subset of the Freddie Mac Single-Family Loan-Level Dataset. It contains about 500,000 rows and is about 80 MB.
Regression Analysis/Regressor Model
Regression tries to predict a continuous number (as opposed to classification, which only categorizes). With a regressor model, you try to predict the exact number from your response column. In our case, we will try to predict the interest rate (a continuous value). You will see later on that some samples might have a 7.5% interest rate, and our regression model will try to predict that number.
There are different types of regression analysis; for example, there is a linear regression, where you fit a straight line to your response based on your predictors, and you try to predict your output with it. Linear regressions are only advised for datasets with a linear distribution. There are also non-linear regressions, which are more useful when you do not have a linear distribution of your response variable.
For regression use cases, H2O supports the following metrics:
- R Squared (R2)
- Mean Squared Error (MSE)
- Root Mean Squared Error (RMSE)
- Root Mean Squared Logarithmic Error (RMSLE)
- Mean Absolute Error (MAE)
In this self-paced course, we'll just focus on the RMSE and MAE.
MSE
The MSE metric measures the average of the squares of the errors or deviations. MSE takes the distances from the points to the regression line (these distances are the "errors") and squaring them to remove any negative signs. MSE incorporates both the variance and the bias of the predictor. MSE also gives more weight to larger differences. The bigger the error, the more it is penalized. For example, if your correct answers are 2,3,4 and the algorithm guesses 1,4,3, then the absolute error on each one is exactly 1, so squared error is also 1, and the MSE is 1. But if the algorithm guesses 2,3,6, then the errors are 0,0,2, the squared errors are 0,0,4, and the MSE is a higher 1.333.
RMSE
The RMSE metric evaluates how well a model can predict a continuous value. The RMSE units are the same as the predicted target, which is useful for understanding if the size of the error is of concern or not. The smaller the RMSE, the better the model's performance. RMSE is sensitive to outliers, meaning that when the error is larger, the more it is penalized.
MAE
The MAE is an average of the absolute errors. The MAE units are the same as the predicted target as well as the RMSW, which is also useful for understanding whether the size of the error is of concern or not. The smaller the MAE, the better the model's performance. MAE is robust to outliers, meaning all errors are penalized equally.
For a detailed description of the other metrics, please check out the H2O-3 Documentation - Evaluation Model Metrics Section
Based-Tree Algorithms
Before we can talk about XGBoost, we first need to talk about Decision Trees and Trees Ensemble.
Decision Trees
Decision trees separate the data into a series of questions, and as the name suggests, it uses a tree-like model of decisions to make a prediction. Decision trees subdivide the dataset and move event outcomes left and right to build the tree model and fit all the data. The series of questions are generated automatically to optimize the separation of the data points depending on what you are trying to find whether you are doing a regression or classification tree.
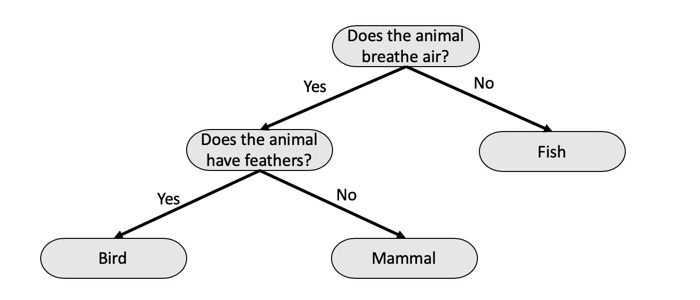
Below is a simple example of a classification tree of looking through three different types of animals. We read the decision trees from top to bottom, and in this case, we can see that the first question is to decide whether the animal is a Fish or not. If the animal is not, then we see another question, which is Does the animal have feathers and depending on the answer to that question, then a decision is made. If the answer is Yes, then the decision tree says the animal is a Bird, but if the animal does not have feathers, then the decision tree says it is a Mammal. Please note that the tree could continue growing if we were trying to find a specific bird or mammal.
Decisions trees have many strengths, such as being non-linear, this is very helpful because many times the datasets are not linear. They are robust to correlated features, meaning correlated features don't really affect their performance. They are also robust to missing values, so if you don't have some values, the trees are okay with that. Decision trees are also easy to understand, and also fast to train and score. However, they do have some weaknesses, and one of them is that when you do have a linear dataset, they are very inefficient when fitting a linear relationship. Also, they are not very accurate when compared to regularized linear models, or deep learning models, and one of the reasons for that is they tend to overfit. For that reason, we need to study tree ensembles, which is one of the solutions to the accuracy issue of decision trees.
Tree Ensembles
Trees Ensembles combine several decision trees in order to solve the same problem and make better predictions. One example of tree ensembles is Random Forest, which uses bagging or bootstrap aggregation, meaning we fit many different trees on different samples of the data. This is done by shuffling the data and growing a tree to obtain a result from it, then the data is shuffled one more time, and then we grow a new tree and combine the results of each of the trees to improve the overall performance. Another example is Gradient Boosting Machines (GBMs), which use boosting. In boosting, the trees are dependent on each other because GBMs fit consecutive trees, each tree solving the net error of the prior tree[1]. So, with GBMs, each tree is fixing up the net error of the entire system. Another example of tree ensembles is eXtreme Gradient Boosting or XGBoost
XGBoost
XGBoost is another decision-tree-based ensemble that uses boosting to yield accurate models. Similarly to the GBMs, XGBoost builds models sequentially, with each new model trying to solve the net error from the previous model. XGBoost provides parallel tree boosting (also known as GBDT, GBM) that solves many data science problems in a fast and accurate manner. For many problems, XGBoost is one of the best GBM frameworks today.
So why H2O's XGBoost?
H2O's XGboost is the same as the regular XGBoost, but using it under H2O, gives you the advantage to use all the features provided by H2O, such as the light data preparation. XGBoost only works with numbers; for that reason, H2O will automatically transform the data into a form that is useful for XGBoost, such as one-hot encode categorical features. H2O will also automatically choose sparse/dense data representation. Since XGBoost, as well as H2O, does in-memory computation, H2O takes advantage of that, and by formatting the data in an acceptable format for XGBoost, as well as doing some optimization, it achieves a fast in-memory computation. Other advantages of H2O's XGBoost is the ease to use, the ability to use H2O GridSearch to tune it, and also easy deployment. On top of that, you can also use Flow to explore your XGBoost model, and it is also one of the models included in H2O's AutoML. If you would like to know more about H2O XGBoost implementation, make sure to check out the Documentation section on XGBoost
Deep Learning
Deep learning is a subset of machine learning that uses neural networks to solve complex problems that other machine learning algorithms have difficulties with, such as image classification, speech recognition, etc. Deep Learning models have an advantage over standard machine learning because they are very effective at learning non-linear derived features from the input features. Neural networks are algorithms based on how the human brain works because they are composed of nodes or commonly known as "neurons," and thus the name of neural networks. One of the simplest neural network architecture is a single layer perceptron. A perceptron takes binary inputs, as shown in the picture below, and produces a single binary output[2].
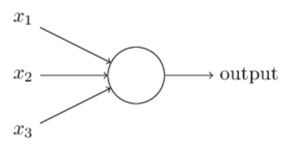
In the figure above, we see a perceptron with three inputs; these inputs are fed into the neuron, which will then decide if the output should be a zero or one. Simply said, a neuron is a function that takes multiple numeric inputs and yields a numeric output. Below is a representation of a more complex neural network
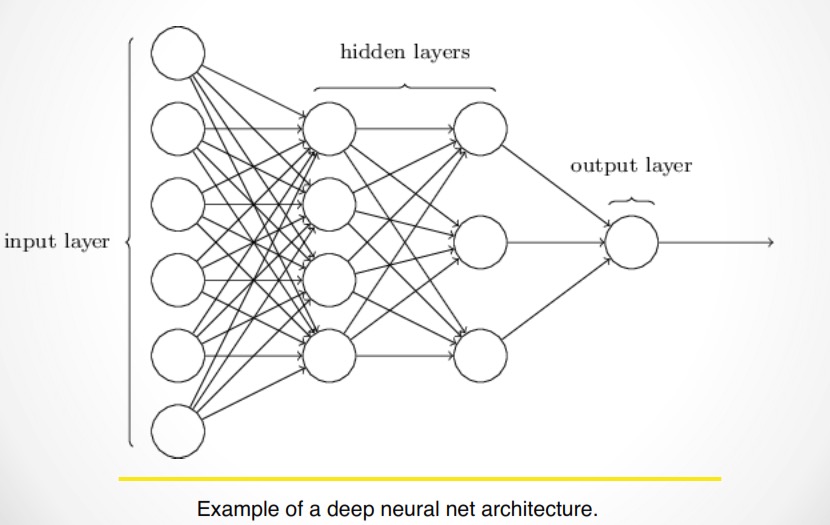
In the image above, you can see a neural network with two hidden layers, and with an input and output layer. We can say that the input layer has six neurons, the first hidden layer has four neurons, while the second hidden layer has 3, and lastly, the output layer has one neuron. A neural network can have as many hidden layers as the user may find suitable. Although deep learning models can solve almost any problem, they tend to be slow and can be hard to use and tune. Nowadays, one of the most popular deep learning frameworks is TensorFlow, as it is an open-source AI library that allows users to create different types of neural networks with many layers. Tensorflow allows you to build Deep Neural Networks(DNNs), which are feedforward multilayer neural networks, among other types of models. TensorFlow also provides DNNs models for classification and for regression use cases as different models.
So why H2O's Deep Learning?
H2O's implementation of Deep Learning is based on a multi-layer feedforward artificial neural network that is trained with stochastic gradient descent using back-propagation. The network can contain a large number of hidden layers consisting of neurons with tanh, rectifier, and maxout activation functions. Advanced features such as adaptive learning rate, rate annealing, momentum training, dropout, L1 or L2 regularization, checkpointing, and grid search enable high predictive accuracy. Although DNNs can be very good at finding different patterns on data, they are not very helpful for image classification. One advantage of H2O implementations is that it is designed to run in parallel across a cluster on very large data. This makes H2O implementation faster than other libraries performing a similar task. Another advantage is that it is fairly easy to use, as the model is instantiated in the same manner as the other H2O estimators. On top of that, you also get the ability to use all the features from H2O with your DNN model. For more information about H2O Deep Learning, make sure you check out the Documentation Section on Deep Learning
Resources
[2] Michael A. Nielsen, "Neural Networks and Deep Learning"
Deeper Dive
Additive Logistic Regression: A statistical view of Boosting
First, let's take a look at the first ten rows of the dataset in our Jupyter Notebook
loan_level.head()
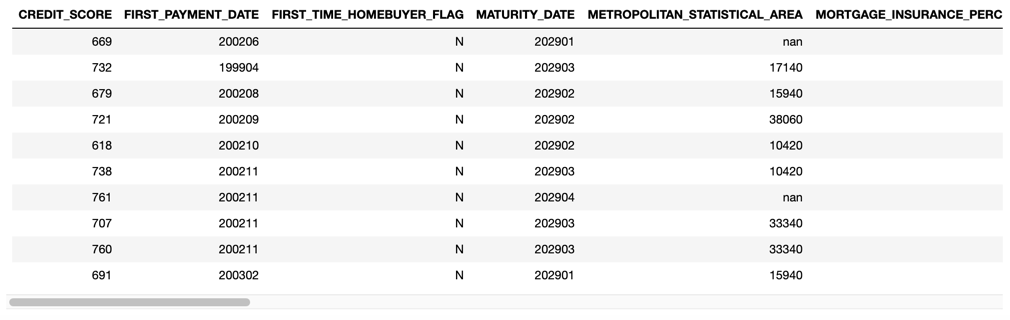
If you scroll to the right, you will see all the columns in the dataset that we are using for this self-paced course.
Now, since we are going to try to predict the interest rate, let's see some information about the ORIGINAL_INTEREST_RATE column.
loan_level["ORIGINAL_INTEREST_RATE"].describe()
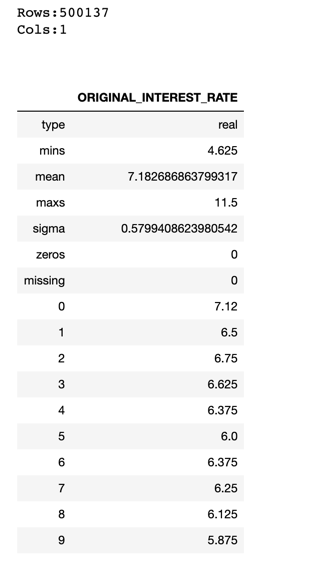
From the description above, we can see that the maximum interest rate value is 11.5%, and the minimum is 4.625%, while the average or mean is 7.183%. Our models will have to predict a numerical value from 4.625 to 11.5 based on the predictors that we choose. Let's take a look at a more graphical representation of our data with a histogram
loan_level["ORIGINAL_INTEREST_RATE"].hist()
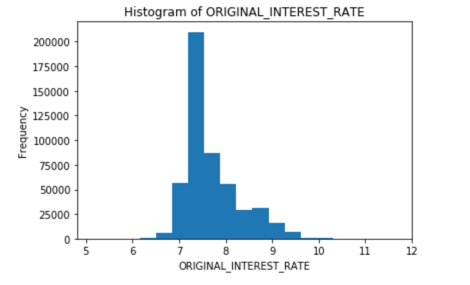
The histogram verifies that the interest rate around 7 and 7.5 is the most frequent one. Now that we have an idea of what our data and our response variable looks like, we can split the dataset.
Please note that the main goal of this self-paced course is to show the usage of some models for regression problems, as well as to tune some of the hyper-parameters of the models. For that reason, we will be skipping any data visualization and manipulation, as well as feature engineering. The aforementioned stages in machine learning are very important, and should always be done; however, they will be covered in later self-paced courses.
We will split the dataset into three sets, training, validation, and test set. The reason for having validation and test sets is because we will use the validation set to tune our models, and we will treat the test set as some unseen data in which we will see how our models perform. We will assign 70% of our data to the training set, and 15% to both the validation and test sets. Split the dataset and print the distribution of each set
train, valid, test = loan_level.split_frame([0.70, 0.15], seed = 42)
print("train:%d valid:%d test:%d" % (train.nrows, valid.nrows, test.nrows))
Output:
train:350268 valid:74971 test:74898
Choose your y variable or response and the x variable, or predictors
y = "ORIGINAL_INTEREST_RATE"
ignore = ["ORIGINAL_INTEREST_RATE",
"FIRST_PAYMENT_DATE",
"MATURITY_DATE",
"MORTGAGE_INSURANCE_PERCENTAGE",
"PREPAYMENT_PENALTY_MORTGAGE_FLAG",
"LOAN_SEQUENCE_NUMBER",
"PREPAID",
"DELINQUENT",
"PRODUCT_TYPE"]
x = list(set(train.names) - set(ignore))
The reason we are ignoring all those columns is that at the time someone would have to decide the interest rate for a loan, they will not have access to that information. For that reason, it would not make sense to train the model with data that will not be available when trying to make predictions. Now we are ready to build our first regression model.
First, let's take a look at the first ten rows of the dataset in our Jupyter Notebook
# Print first 10 rows of the data
h2o.head(loan_level, n = 10)
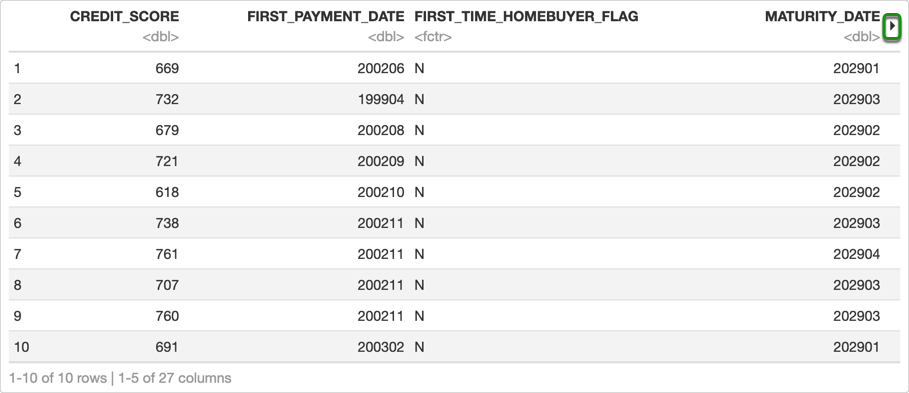
If you click the arrow in the top right corner, you will see the other columns in the dataset that we are using for this self-paced course.
Now, since we are going to try to predict the interest rate, let's see some information about the ORIGINAL_INTEREST_RATE column.
# Print a statistical description of the data
h2o.describe(loan_level[, c("ORIGINAL_INTEREST_RATE")])
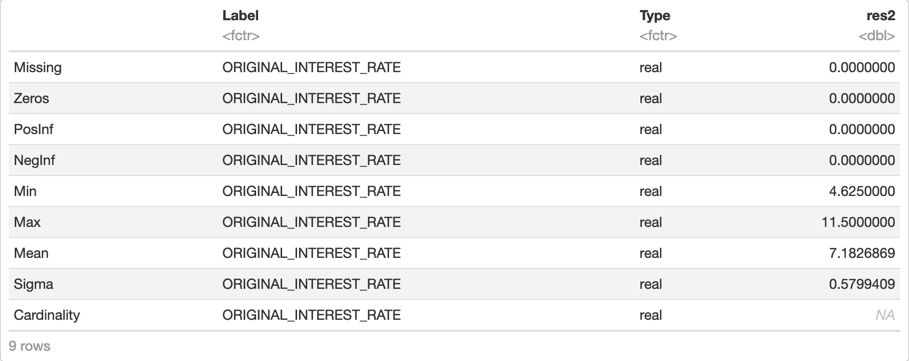
From the description above, we can see that the maximum interest rate value is 11.5%, and the minimum is 4.625%, while the average or mean is 7.183%. Our models will have to predict a numerical value from 4.625 to 11.5 based on the predictors that we choose. Let's take a look at a more graphical representation of our data with a histogram
# Plot a histogram of the response column
h2o.hist(loan_level[, c("ORIGINAL_INTEREST_RATE")])
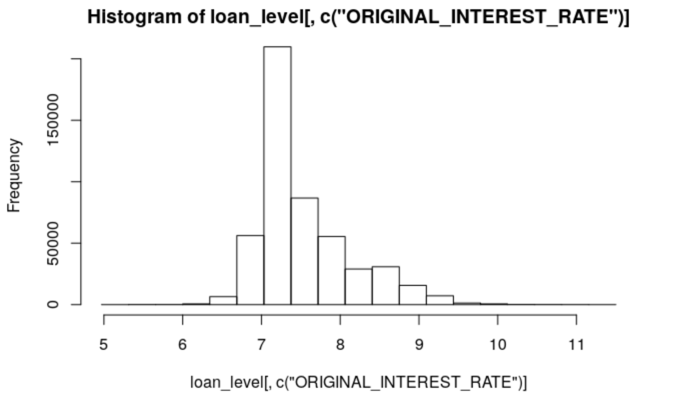
The histogram verifies that the interest rate around 7 and 7.5 is the most frequent one. Now that we have an idea of what our data and our response variable looks like, we can split the dataset.
Please note that the main goal of this self-paced course is to show the usage of some models for regression problems, as well as to tune some of the hyper-parameters of the models. For that reason, we will be skipping any data visualization and manipulation, as well as feature engineering. The aforementioned stages in machine learning are very important, and should always be done; however, they will be covered in later self-paced courses.
We will split the dataset into three sets, training, validation, and test set. The reason for having validation and test sets is because we will use the validation set to tune our models, and we will treat the test set as some unseen data in which we will see how our models perform. We will assign 70% of our data to the training set, and 15% to both the validation and test sets. Split the dataset and print the distribution of each set
# Split data into train, val
splits <- h2o.splitFrame(loan_level, c(0.7, 0.15), seed = 42)
train <- splits[[1]]
valid <- splits[[2]]
test <- splits[[3]]
dim(train)
350268 27
dim(valid)
74971 27
dim(test)
74898 27
Choose your y variable or response and the x variable, or predictors
# Identify predictors and response
ignore <- c("ORIGINAL_INTEREST_RATE", "FIRST_PAYMENT_DATE", "MATURITY_DATE",
"MORTGAGE_INSURANCE_PERCENTAGE", "PREPAYMENT_PENALTY_MORTGAGE_FLAG",
"LOAN_SEQUENCE_NUMBER", "PREPAID", "DELINQUENT", "PRODUCT_TYPE")
y <- "ORIGINAL_INTEREST_RATE"
x <- setdiff(colnames(train), ignore)
x
Output
[1] "CREDIT_SCORE" "FIRST_TIME_HOMEBUYER_FLAG" "METROPOLITAN_STATISTICAL_AREA"
[4] "NUMBER_OF_UNITS" "OCCUPANCY_STATUS" "ORIGINAL_COMBINED_LOAN_TO_VALUE"
[7] "ORIGINAL_DEBT_TO_INCOME_RATIO" "ORIGINAL_UPB" "ORIGINAL_LOAN_TO_VALUE"
[10] "CHANNEL" "PROPERTY_STATE" "PROPERTY_TYPE"
[13] "POSTAL_CODE" "LOAN_PURPOSE" "ORIGINAL_LOAN_TERM"
[16] "NUMBER_OF_BORROWERS" "SELLER_NAME" "SERVICER_NAME"
The reason we are ignoring all those columns is that at the time someone would have to decide the interest rate for a loan, they will not have access to that information. For that reason, it would not make sense to train the model with data that will not be available when trying to make predictions. Now we are ready to build our first regression model.
To use the XGBoost estimator, we can just define a random seed (for reproducibility purposes) and the model ID, in case we wanted to save the model and then retrieve it, or to easily access it in Flow. As we mentioned before, we will be tuning our models with the validation set; however, we could also get a validation score using k-fold cross validation from H2O. We will show you how you would use the k-fold cross-validation, but we are going to use the validation set approach because when training the models, and doing the grid search, it will be much faster than using the k-fold cross-validation approach.
To build your default XGBoost model and to train it, just run the following two lines of code:
xgb = H2OXGBoostEstimator(seed = 42,
model_id = 'XGBoost',
nfolds = 0,
keep_cross_validation_predictions = False)
%time xgb.train(x = x, y = y, training_frame = train, validation_frame = valid)
Note: You do not need to specify the cross-validation parameters, but we want to show the parameters that you would have to change in order to enable H2O internal cross-validation. If you wanted to use the H2O cross-validation, you would have to set keep_cross_validation_predictions to True and change nfolds to 3, 5, or 10, depending on the number of folds that you want; by doing cross-validation, you no longer need a validation frame.
After the XGBoost model is done training, you can print the model summary just by typing the name of your model in a new cell and running it as shown below:
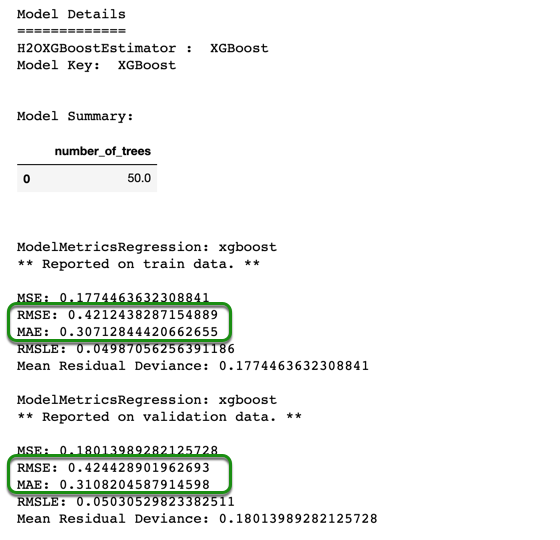
When printing the model summary, you will see a complete summary with some of the parameters in your model (in this case, we only see the number of trees). You will see some scoring metrics on your training data, as well as on your validation data, as shown in the image above. From the summary, we can see that the MAE, in fact, is lower than the RMSE, this might be due to having some of the interest rates at the far end of our range (such as interest rates as high as 10 and 11, when our mean is 7.2). The training and validation RMSE are 0.4212 and 0.4244, respectively. This means that according to the RMSE, on average, the predictions are 0.42 percent off from the actual values. While the training and validation MAE are 0.3071 and 0.3108 respectively, which tells us that the predictions are about 0.31 percent off from the actual values, according to the MAE. Since we have a target interest rate range between 4 to 12 percent, we will try to reduce the RMSE when tuning our models as it will penalize larger errors or outliers.
In the model summary, you will also see two tables; the first table is the scoring history, and the second one is the variable importance table (not shown here). Besides looking at the table, we can also take a look at both graphing representations of the scoring history and the variable importance.
Let's first plot the scoring history.
xgb.plot()
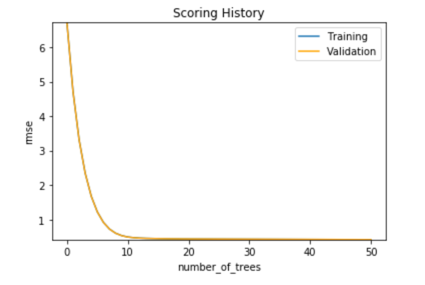
In the plot above, it seems as if only one score is plotted, but that is so because both scores are so close to each other, and you can confirm this by looking at the scoring history table from the model summary.
We can also print the variable importance plot as follow,
xgb.varimp_plot()
You should see an image similar to the one below
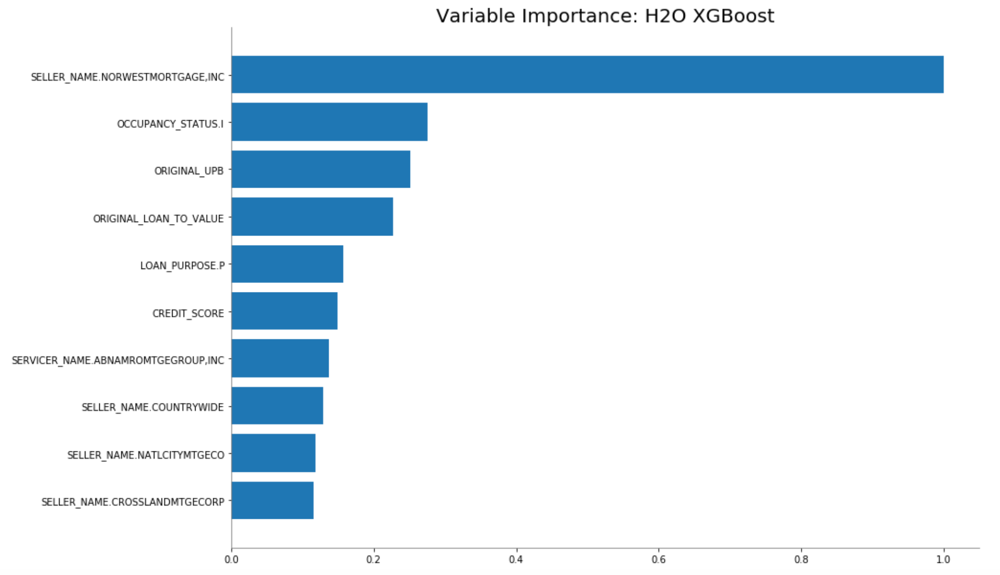
We will make some predictions on our validation set. To compare the predictions to the actual value, we are going to combine the two data frames, the predictions and the validation set, as follow:
xgb_def_pred = xgb.predict(valid)
xgb_def_pred.cbind(valid['ORIGINAL_INTEREST_RATE'])
You will see a table like the one below
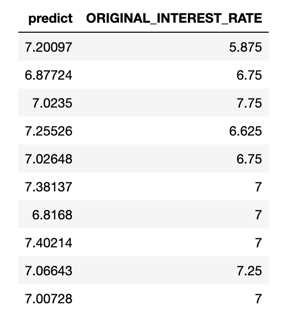
In the first ten predictions, we can see that they are somewhat close to the actual value, except for the first sample, which is more than 1.5% off. We can see that samples such as this one, might make the RMSE higher than the MAE, because of the penalty added in the RMSE calculation.
We can also check the model performance with a test, or in this case, with a validation set, and print some of the scores for our model. For now, we will just save the model performance, as we will use later on.
default_xgb_per = xgb.model_performance(valid)
We will now build our next model.
To use the XGBoost estimator, we can just define a random seed (for reproducibility purposes) and the model ID, in case we wanted to save the model and then retrieve it, or to easily access it in Flow. As we mentioned before, we will be tuning our models with the validation set; however, we could also get a validation score using k-fold cross validation from H2O. We will show you how you would use the k-fold cross-validation, but we are going to use the validation set approach because when training the models, and doing the grid search, it will be much faster than using the k-fold cross-validation approach.
To build your default XGBoost model, and to print a summary of it, just run the following two lines of code:
# Train a default XGBoost
xgb <- h2o.xgboost(x = x,
y = y,
training_frame = train,
model_id = "default_xgb",
validation_frame = valid,
seed = 42)
summary(xgb)
Note: You do not need to specify the cross-validation parameters, but we want to show the parameters that you would have to change in order to enable H2O internal cross-validation. If you wanted to use the H2O cross-validation, you would have to set keep_cross_validation_predictions to True and change nfolds to 3, 5, or 10, depending on the number of folds that you want; by doing cross-validation, you no longer need a validation frame.

When printing the model summary, you will see a complete summary with some of the parameters in your model (in this case, we only see the number of trees). You will see some scoring metrics on your training data, as well as on your validation data, as shown in the image above. From the summary, we can see that the MAE, in fact, is lower than the RMSE, this might be due to having some of the interest rates at the far end of our range (such as interest rates as high as 10 and 11, when our mean is 7.2). The training and validation RMSE are 0.4212 and 0.4244, respectively. This means that according to the RMSE, on average, the predictions are 0.42 percent off from the actual values. While the training and validation MAE are 0.3071 and 0.3108 respectively, which tells us that the predictions are about 0.31 percent off from the actual values, according to the MAE. Since we have a target interest rate range between 4 to 12 percent, we will try to reduce the RMSE when tuning our models as it will penalize larger errors or outliers.
In the model summary, you will also see two tables; the first table is the scoring history, and the second one is the variable importance table (not shown here). Besides looking at the table, we can also take a look at the variable importance:
# Print the variable importance of the XGBoost
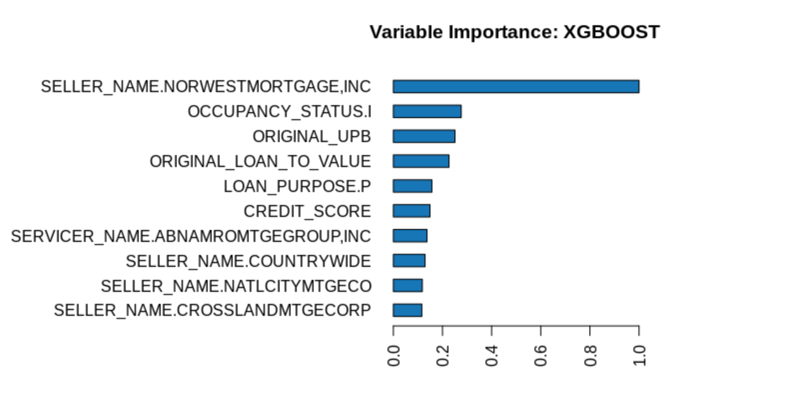
h2o.varimp_plot(xgb)
You should see an image similar to the one below:
We will make some predictions on our validation set. To compare the predictions to the actual value, we are going to combine the two data frames, the predictions and the validation set, as follow:
# Make predictions with the default model
xgb_def_pred <- h2o.predict(xgb, valid)
# Combine the predictions with the actual response
h2o.cbind(xgb_def_pred, valid[, c("ORIGINAL_INTEREST_RATE")])
You will see a table like the one below
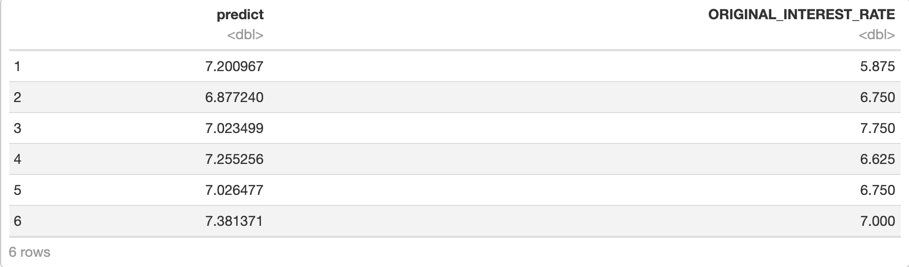
Note: We are printing the default number of rows for our predictions frame. However, if you want to see more rows, you can use the .head() function and adjust the value of n the same way we did when we printed the first ten rows of the dataset at the beginning of this self-paced course.
In the first six predictions, we can see that they are somewhat close to the actual value, except for the first sample, which is more than 1.5% off. We can see that samples such as this one, might make the RMSE higher than the MAE, because of the penalty added in the RMSE calculation.
We can also check the model performance with a test, or in this case, with a validation set, and print some of the scores for our model. For now, we will just save the model performance, as we will use later on.
# Save the validation model performance of the default model
valid_def_xgb_perf <- h2o.performance(xgb, valid)
We will now build our next model.
We can also build the XGBoost Model in Flow. In the first self-paced course, we showed how to load a dataset into Flow and how to split it. However, the data frames that we have in our Jupyter Notebook and RStudio are also stored in Flow, and we will use it to build our XGBoost model in Flow.
In your Flow instance, go to the Assistance menu, and click on getFrames as shown below:
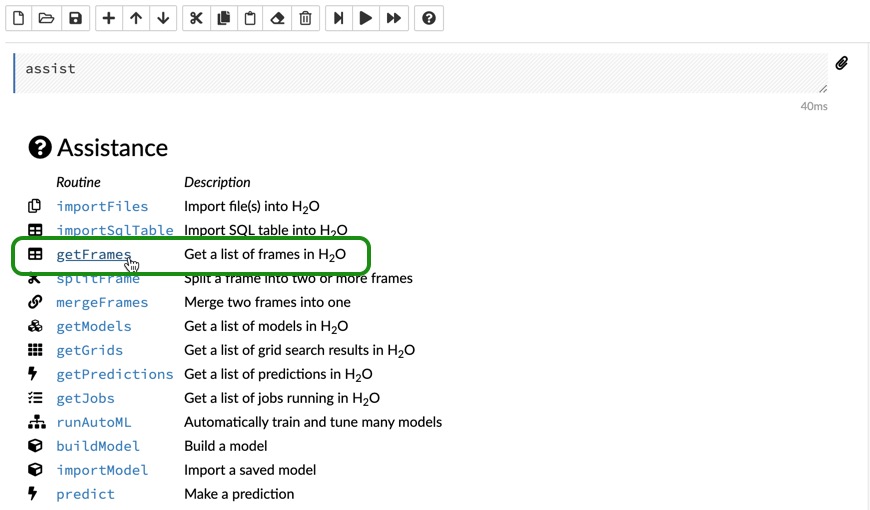
Now, you should see a list of data frames, with all your data frames from the Jupyter Notebook. Look for the data frame with about 350,000 rows and 27 columns, which is our train frame. You have three options for each frame, Build Model, which lets you build a model using that data frame. Predict, which lets you make predictions if you already have a model and Inspect, which lets you take a quick look at your data frame. Click on Build Model
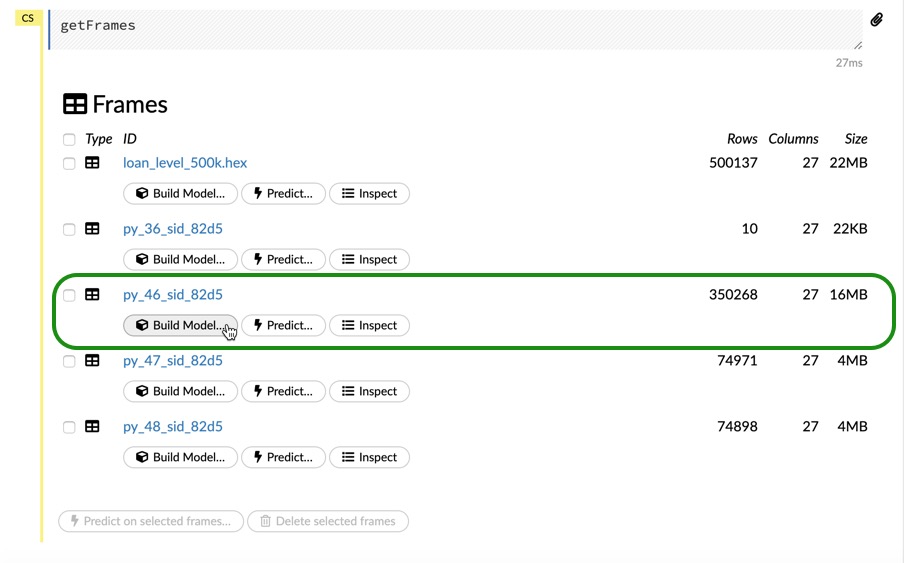
Note: If you need to import your dataset into your Flow instance, please refer to Task 3 of Introduction to Machine Learning with H2O-3 - Classification and click on the Flow tab for instructions on how to import your dataset and how to split it.
Once you click on Build Model in your data frame, you should see the following:
From the dropdown menu, choose XGBoost, then change the model_id to flow_xgb. Leave the training and validation frame as they are. For our Flow model, we will use H2O cross-validation, just so that we can see both types of cross-validation. For the response_column choose ORIGINAL_INTEREST_RATE. Next, for the ignored_columns make sure that the following 8 columns are selected:
FIRST_PAYMENT_DATEMATURITY_DATEMORTGAGE_INSURANCE_PERCENTAGE,PREPAYMENT_PENALTY_MORTGAGE_FLAG,PRODUCT_TYPE.LOAN_SEQUENCE_NUMBER,PREPAID,DELINQUENT
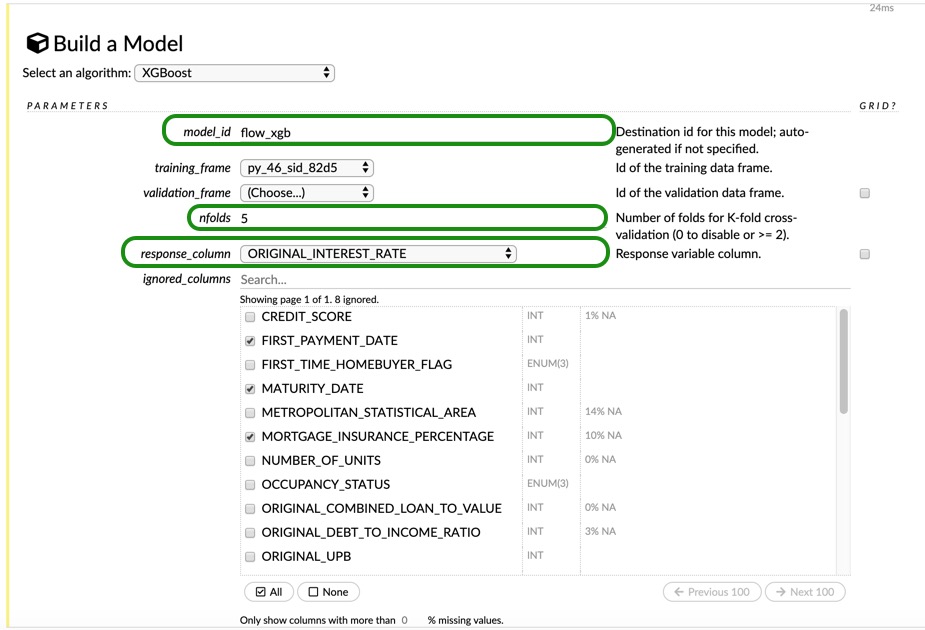
You can change the seed to 42 as well. Leave everything else as-is, and scroll all the way down and click on Build Model. Once your model is done click on View
You should be able to see the model parameters, the scoring history, the variable importance plot, and all the outputs regarding your model.
Deep learning models are not reproducible, meaning they won't yield the same result every time you run the same experiment. For that reason, please don't expect to get exactly the same results. However, for the H2O-3 Deep Learning model, you can set the parameter reproducible=True which will force reproducibility on small datasets. The disadvantage of this parameter is that in order to be reproducible, it only uses one thread and thus the model takes more time to be trained. We will use this parameter towards the end of this self-paced course.
As mentioned before, the deep learning estimator is fairly easy to use. For our default Deep Learning model, we do not need to define any parameters, but we will define the seed, model id, and we will also make sure that cross-validation is disabled, as we are already using a validation frame.
dl = H2ODeepLearningEstimator(seed = 42,
model_id = 'DL',
nfolds = 0,
keep_cross_validation_predictions = False)
%time dl.train(x = x, y = y, training_frame = train, validation_frame = valid)
Print the summary of the model, and notice how the RMSE and MAE are higher than those of the default XGBoost model.
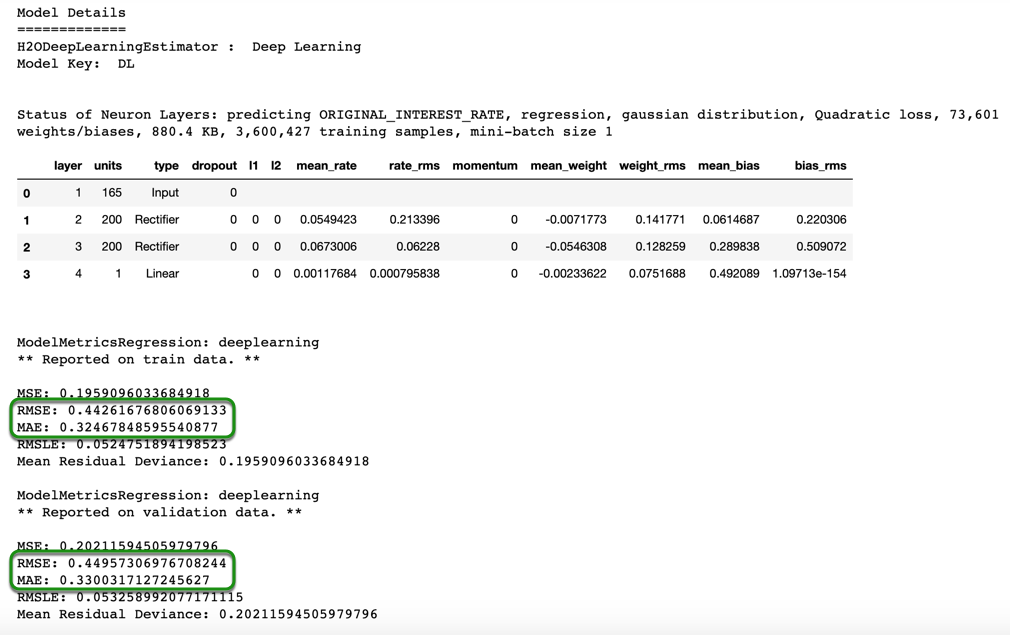
For our deep learning model, we see that our validation scores are higher than the training scores, but not by much. The training and validation RMSE scores are 0.4426 and 0.4495, respectively. And the training and validation MAE are 0.3247 and 0.3300, respectively. You can also see the scoring history and variable importance table. We can also plot both the scoring history and variable importance of our model.
dl.plot()
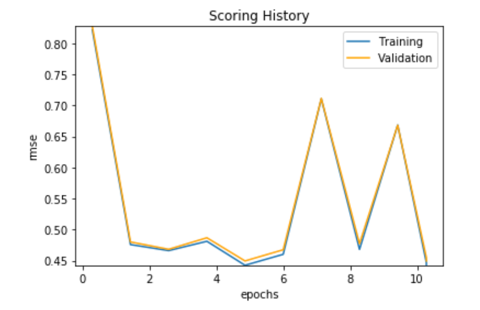
Please note that your plot will not look exactly the same as the one above.
If you want to look at the exact number of epochs, you can do so as shown below:
print("epochs = ", dl.params['epochs'])
Output:
epochs = {'default': 10.0, 'actual': 10.0}
In case you want to look at other parameters, you can just change the parameter inside the brackets in dl.params[]
The default number of epochs for a Deep Learning model is 10. We will try to find a number of epochs that will give us a better score when we tune our model.
Let's take a quick look at the variable importance plot to see how it compares to the variable importance plot from our XGBoost model.
dl.varimp_plot()
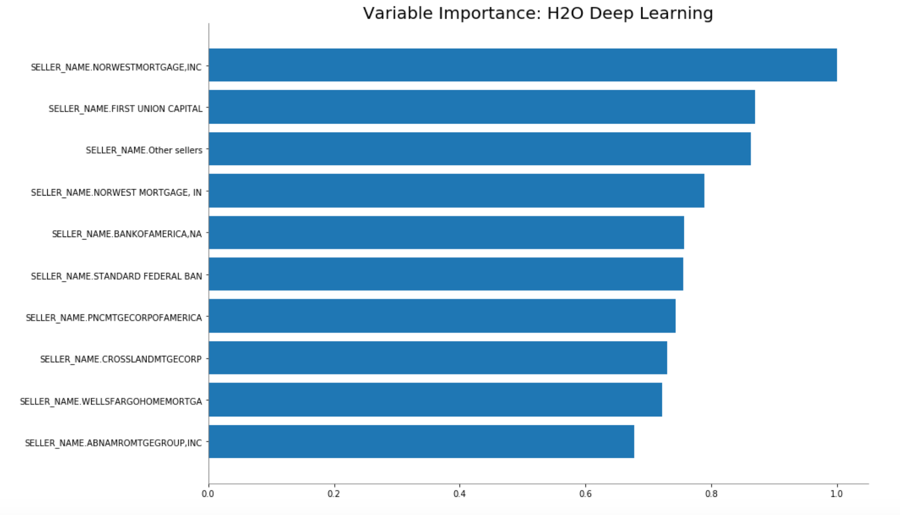
As we can see in the image above, the variable importance plot changes a lot compared to the XGBoost. For our Deep Learning model, we see most of the SELLER_NAME variables, and the most important variable for our Deep Learning model "Other sellers" is not even included in the top ten for the XGBoost. Also, the top 10 most important variables for the Deep Learning model have almost the same significance, as opposed to the other model.
Save the model performance on the validation set, as we will use it later on for comparison purposes.
default_dl_per = dl.model_performance(valid)
Deep learning models are not reproducible, meaning they won't yield the same result every time you run the same experiment. For that reason, please don't expect to get exactly the same results. However, for the H2O-3 Deep Learning model, you can set the parameter reproducible=True which will force reproducibility on small datasets. The disadvantage of this parameter is that in order to be reproducible, it only uses one thread and thus the model takes more time to be trained. We will use this parameter towards the end of this self-paced course.
As mentioned before, the deep learning estimator is fairly easy to use. For our default Deep Learning model, we do not need to define any parameters, but we will define the seed, model id, and we will also make sure that cross-validation is disabled, as we are already using a validation frame.
# Train a Deep Learning Model
dl <- h2o.deeplearning(x = x,
y = y,
training_frame = train,
model_id = "default_dl",
validation_frame = valid,
seed = 42)
dl
Print the summary of the model, and notice how the RMSE and MAE are higher than those of the default XGBoost model.
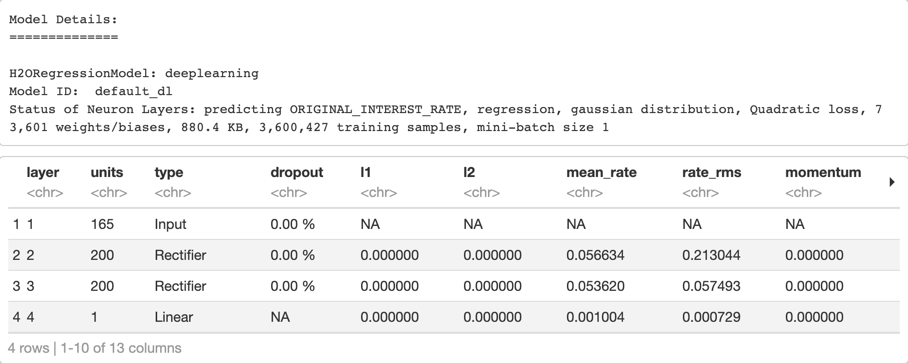

For our deep learning model, we see that our validation scores are higher than the training scores, but not by much. The training and validation RMSE scores are 0.4388 and 0.4434, respectively. And the training and validation MAE are 0.3237 and 0.3277, respectively. You can also see the scoring history and variable importance table. Next, we will plot both the scoring history and variable importance of our model.
# Plot the scoring history for the DL model
plot(dl)
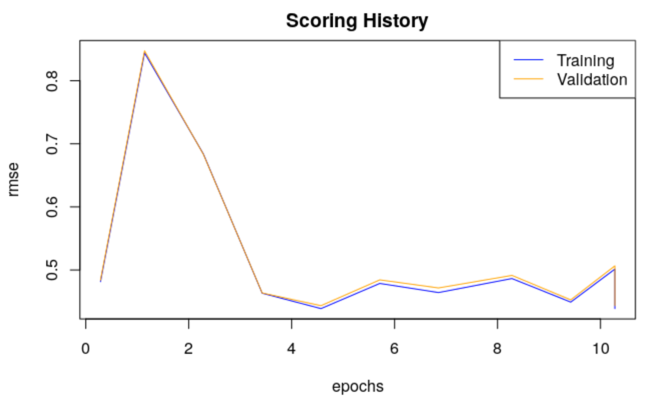
Please note that your plot will not look exactly the same as the one above.
If you want to look at the exact number of epochs, you can do so as shown below:
# Retrieve the number of epochs and hidden layers of the model
dl@allparameters[["epochs"]]
Output:
10
The default number of epochs for a Deep Learning model is 10. We will try to find a number of epochs that will give us a better score when we tune our model.
Let's take a quick look at the variable importance plot to see how it compares to the variable importance plot from our XGBoost model.
dl.varimp_plot()

As we can see in the image above, the variable importance plot changes a lot compared to the XGBoost. For our Deep Learning model, we see most of the SELLER_NAME variables, and one of the most important variable for our Deep Learning model Other sellers is not even included in the top ten for the XGBoost. Also, the top 10 most important variables for the Deep Learning model have almost the same significance, as opposed to the other model.
You could make the predictions on the validation frame the same way we did for the XGBoost, and it's as follow:
# Make predictions on the validation set
dl_def_pred <- h2o.predict(dl, valid)
# Compare the predictions to the actual response column
h2o.cbind(dl_def_pred, valid[, c("ORIGINAL_INTEREST_RATE")])
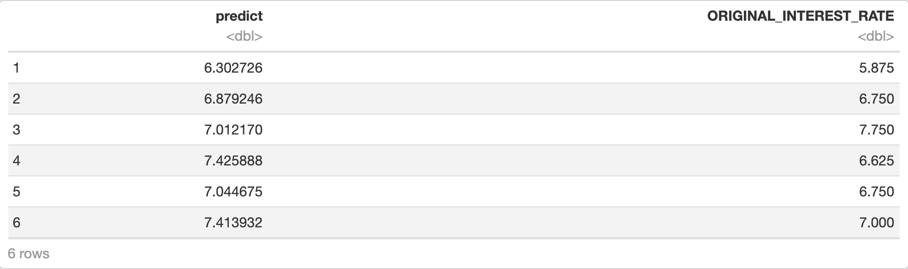
As we can see in the image above, the predictions are also close to the actual value. We will try to improve the predictions by tuning our model.
Save the model performance on the validation set, as we will use it later for comparison purposes.
# Save the validation model performance
valid_def_dl_perf <- h2o.performance(dl, valid)
To build a Deep Learning model in Flow, you can follow the same instructions as for the XGBoost. Find the training set (you could use the entire dataset since we are using H2O cross-validation, but it would not be a fair comparison, as the model in Flow would be training on more data) click on Build Model, then select Deep Learning for the "Select an algorithm" section. Then, change the model_id, change nfolds from 0 to 5. Select ORIGINAL_INTEREST_RATE as the response_column and check the following 8 columns for the ingored_columns section
FIRST_PAYMENT_DATE,MATURITY_DATE,MORTGAGE_INSURANCE_PERCENTAGE,PREPAYMENT_PENALTY_MORTGAGE_FLAG,PRODUCT_TYPE,LOAN_SEQUENCE_NUMBER,PREPAID,DELINQUENT.
You can leave everything else as-is, and click on Build Model. Wait for it to be done, and explore the outputs. How do they compare to the results we obtained from the Jupyter Notebook or RNotebook? Are the validation scores similar?
We will use H2O GridSearch to find the best parameters for our XGBoost.
Note: If you are not sure what H2O GridSearch is, or how it works, please refer to Task 7 of Introduction to Machine Learning with H2O-3 - Classification, or go to Grid Search Section of the H2O documentation.
We will first try to find the max_depth for our XGBoost, as this is one of the most important parameters for an XGBoost model.
max_depth defines the number of nodes along the longest path from the start of the tree to the farthest leaf node. By default, the value is 6. We could do a random search along with the other parameters, but when max_depth is large, the model takes longer to train; therefore, in order to do a more efficient random search with the other parameters, we will first find the best value max_depth, and we will use 100 trees with early stopping to tune our hyper-parameters.
xgb = H2OXGBoostEstimator(model_id = 'xgb',
ntrees = 300,
stopping_rounds = 3, #default
stopping_tolerance = 1e-3, #default
stopping_metric = "rmse", #default
seed = 42)
hyper_params = {'max_depth' : [5,7,9,10,12,13,15,20]}
grid_id = 'max_depth_grid'
search_criteria = { "strategy":"Cartesian"}
xgb_grid = H2OGridSearch(model = xgb,
hyper_params = hyper_params,
grid_id = grid_id,
search_criteria = search_criteria)
%time xgb_grid.train(x = x, y = y, training_frame = train, validation_frame = valid)
We can get the models trained by the GridSearch with the .get_grid() function, and print it in a nice table format with .sorted_metric_table() function.
sorted_xgb = xgb_grid.get_grid(sort_by = 'rmse', decreasing = False)
sorted_xgb.sorted_metric_table()
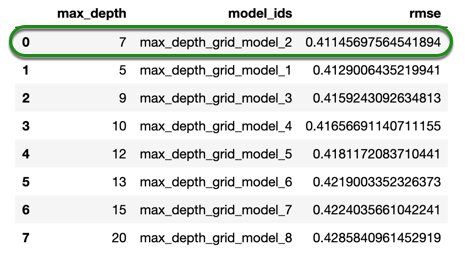
We will use four values for max_depth based on the results from the previous grid search to try to tune the next parameters. We will set ntrees=500 while using early stopping, the same way we did in the first self-paced course and we will try to tune the following three parameters:
1. sample_rate: Specifies the row sampling ratio of the training instance (x-axis). (Note that this method is sample without replacement.) For example, setting this value to 0.5 tells XGBoost to randomly collecte half of the data instances to grow trees. This value defaults to 1, and the range is 0.0 to 1.0. Higher values may improve training accuracy. Test accuracy improves when either columns or rows are sampled.
2. col_sample_rate: Specifies the column sampling rate (y-axis) for each split in each level. (Note that this method is sample without replacement.) This value defaults to 1.0, and the range is 0.0 to 1.0
3. col_sample_rate_per_tree: Specifies the column subsampling rate per tree. (Note that this method is sample without replacement.) This value defaults to 1.0 and can be a value from 0.0 to 1.0
Since we have 4 parameters in this grid search, we will be doing a random search; we will be using early stopping, and for our stopping criteria, we will set a limit of 100 models or 15 minutes. You can change these settings in the search_criteria_tune parameter for the grid search.
xgb = H2OXGBoostEstimator(model_id = 'xgb_grid',
ntrees = 500,
learn_rate = 0.25,
stopping_rounds = 3, #default
stopping_tolerance = 1e-3, #default
stopping_metric = "rmse", #default
seed = 42)
hyper_params = {'max_depth' : [5,6,7,9],
'sample_rate': [x/100. for x in range(20,101)],
'col_sample_rate' : [x/100. for x in range(20,101)],
'col_sample_rate_per_tree': [x/100. for x in range(20,101)]}
search_criteria_tune = {'strategy': "RandomDiscrete",
'max_runtime_secs': 900, #15 min
'max_models': 100, ## build no more than 100 models
'seed' : 42}
xgb_grid = H2OGridSearch(xgb, hyper_params,
grid_id = 'random_grid',
search_criteria = search_criteria_tune)
%time xgb_grid.train(x = x, y = y, training_frame = train, validation_frame = valid)
Let's print the results of our random search:
sorted_xgb = xgb_grid.get_grid(sort_by = 'rmse', decreasing = False)
sorted_xgb.sorted_metric_table()
Please note that the results might not be exactly the same.
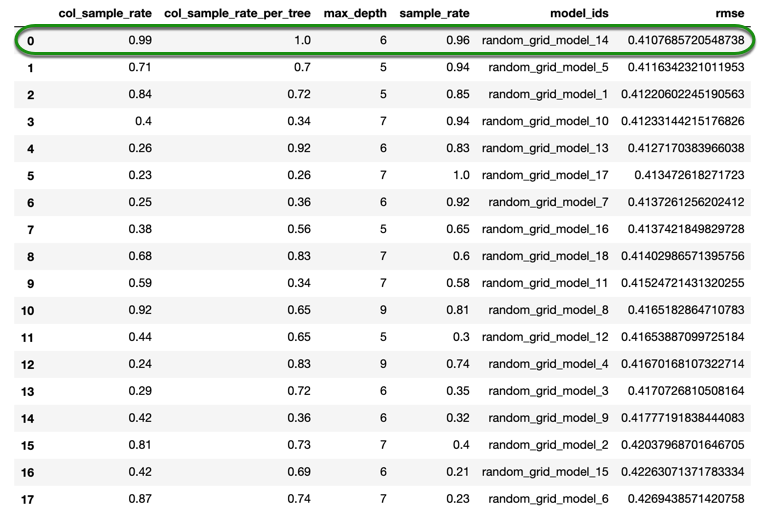
With the grid search that we just did, we were able to train a total of 18 models. The score slightly improved from what we obtained in the first grid search. If we were trying to find the best model, we would need to run the grid search for a longer period of time, that way more models can be trained. We could also do a local search with the values we just found and see if we could get better results, but for the purpose of this self-paced course, we will stop here.
Let's retrieve the best model from the grid search and then compare the results from the default model to the tuned model. In order to do so, we also need to save the performance of the best model on the validation set.
Retrieve the best model from the grid search
best_xgb_model = xgb_grid.models[0]
best_xgb_model
Please note that you can also retrieve any of your models by changing the number inside the brackets. Now save the model performance on the validation set.
tuned_xgb_per = best_xgb_model.model_performance(valid)
Print both RMSE and MAE
print("Default XGB RMSE: %.4f \nTuned XGB RMSE:%.4f" % (default_xgb_per.rmse(), tuned_xgb_per.rmse()))
Output:
Default XGB RMSE: 0.4244
Tuned XGB RMSE:0.4108
Our RMSE slightly improved with the tuning that we did. As we mentioned before, we only let each random search run for 15 minutes. To see if we can obtain a much better model, we would have to let it run for much longer that way more models can be trained.
We will check the MAE now:
print("Default XGB MAE: %.4f \nTuned XGB MAE:%.4f" % (default_xgb_per.mae(), tuned_xgb_per.mae()))
Output:
Default XGB MAE: 0.3108
Tuned XGB MAE:0.2986
In the case of an interest rate decision, an MAE of 0.30 is good enough as it tells us that, on average, the model would predict a very close interest rate to what someone with "x" characteristics should get. However, for some use cases an MAE of 0.30 might be too high, so it all depends on the application to decide whether or not our MAE results are satisfactory. We will see if the Deep Learning model can yield a lower RMSE and MAE.
We will use H2O GridSearch to find the best parameters for our XGBoost.
Note: If you are not sure what H2O GridSearch is, or how it works, please refer to Task 7 of Introduction to Machine Learning with H2O-3 - Classification, or go to Grid Search Section of the H2O documentation.
We will first try to find the max_depth for our XGBoost, as this is one of the most important parameters for an XGBoost model.
max_depth defines the number of nodes along the longest path from the start of the tree to the farthest leaf node. By default, the value is 6. We could do a random search along with the other parameters, but when max_depth is large, the model takes longer to train; therefore, in order to do a more efficient random search with the other parameters, we will first find the best value max_depth, and we will use 100 trees with early stopping to tune our hyper-parameters.
# Set-up the Grid Search
xgb_depth_grid <- h2o.grid(algorithm = "xgboost",
grid_id = "xgb_depth_grid",
stopping_rounds = 3,
stopping_metric ="RMSE",
stopping_tolerance = 1e-3,
seed = 42,
ntrees = 300,
x = x,
y = y,
training_frame = train,
validation_frame = valid,
hyper_params = list(
max_depth = c(5,7,9,10,12,13,15,20)),
search_criteria = list(
strategy = "Cartesian"))
We can get the models trained by the GridSearch with the .getGrid() function, and print it in a nice table format with as.data.frame.
# Retrieve the grid search sorted by RMSE and in ascending order
xgb_depth_grid_rmse <- h2o.getGrid(grid_id = "xgb_depth_grid", sort_by = "rmse", decreasing = FALSE)
as.data.frame(xgb_depth_grid_rmse@summary_table)
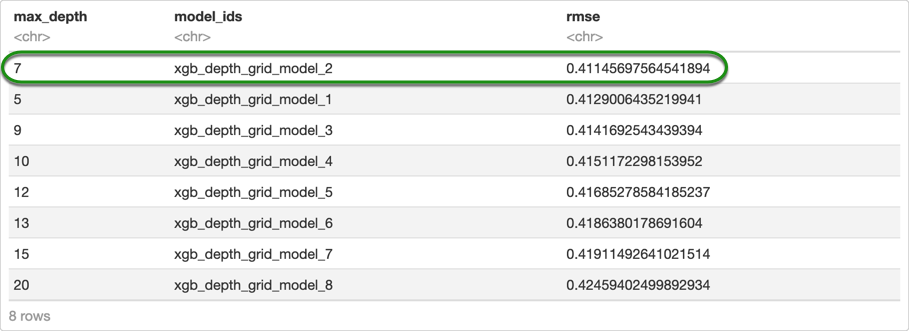
We will use four values for max_depth based on the results from the previous grid search to try to tune the next parameters. We will set ntrees=500 while using early stopping, the same way we did in the first self-paced course and we will try to tune the following three parameters:
1. sample_rate: Specifies the row sampling ratio of the training instance (x-axis). (Note that this method is sample without replacement.) For example, setting this value to 0.5 tells XGBoost to randomly collecte half of the data instances to grow trees. This value defaults to 1, and the range is 0.0 to 1.0. Higher values may improve training accuracy. Test accuracy improves when either columns or rows are sampled.
2. col_sample_rate: Specifies the column sampling rate (y-axis) for each split in each level. (Note that this method is sample without replacement.) This value defaults to 1.0, and the range is 0.0 to 1.0
3. col_sample_rate_per_tree: Specifies the column subsampling rate per tree. (Note that this method is sample without replacement.) This value defaults to 1.0 and can be a value from 0.0 to 1.0
Since we have 4 parameters in this grid search, we will be doing a random search; we will be using early stopping, and for our stopping criteria, we will set a limit of 100 models or 15 minutes. You can change these settings in the search_criteria_tune parameter for the grid search.
# Create sequences for three different parameters to explore more models
xgb_sample_rate <- seq(from = 0.2, to = 1, by = 0.01)
xgb_col_sample_rate <- seq(from = 0.2, to = 1, by = 0.01)
xgb_col_sample_rate_per_tree <- seq(from = 0.2, to = 1, by = 0.01)
xgb_random_grid <- h2o.grid(algorithm = "xgboost",
grid_id = "xgb_random_grid",
stopping_rounds = 3,
stopping_metric = "RMSE",
stopping_tolerance = 1e-3,
seed = 42,
ntrees = 500,
learn_rate = 0.25,
x = x,
y = y,
training_frame = train,
validation_frame = valid,
hyper_params = list(
max_depth = c(5,6,7,9),
sample_rate = xgb_sample_rate,
col_sample_rate = xgb_col_sample_rate,
col_sample_rate_per_tree = xgb_col_sample_rate_per_tree),
search_criteria = list(
strategy = "RandomDiscrete",
max_runtime_secs = 900,
seed = 42))
Let's print the results of our random search:
# Retrieve the second Grid Search for the XGBoost
xgb_random_grid_rmse <- h2o.getGrid(grid_id = "xgb_random_grid", sort_by = "rmse", decreasing = FALSE)
as.data.frame(xgb_random_grid_rmse@summary_table)
Please note that the results might not be exactly the same.
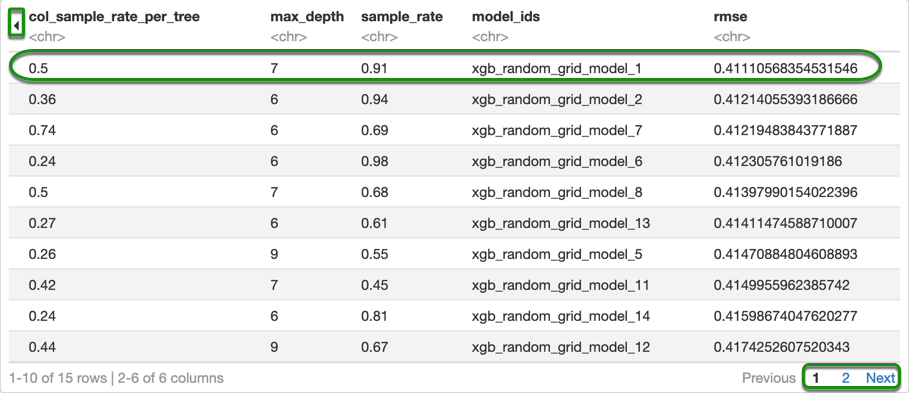
Note: You can look at the other columns of the table by clicking on the arrow in the top left corner. You can also look at the other models that were trained by clicking next or the number "2" in the bottom left corner.
With the grid search that we just did, we were able to train a total of 15 models. The score slightly improved from what we obtained in the first grid search. If we were trying to find the best model, we would need to run the grid search for a longer period of time, that way more models can be trained. We could also do a local search with the values we just found and see if we could get better results, but we will stop here.
Let's retrieve the best model from the grid search and then compare the results from the default model to the tuned model. In order to do so, we also need to save the performance of the best model on the validation set.
Retrieve the best model from the grid search
# Retrieve the best model from the Grid Search
tuned_xgb <- h2o.getModel(xgb_random_grid_rmse@model_ids[[1]]) #getting the best model
Please note that you can also retrieve any of your models by changing the number inside the brackets. Now save the model performance on the validation set.
# Save the validation performance of the tuned model
valid_tuned_xgb_perf <- h2o.performance(tuned_xgb, valid)
Print both RMSE and MAE
# Compare the RMSE of the default and tuned XGBoost
h2o.rmse(valid_def_xgb_perf)
h2o.rmse(valid_tuned_xgb_perf)
Output:
0.4244289
0.4111057
Our RMSE slightly improved with the random grid search that we did. As we mentioned before, we only allowed each random search run for 15 minutes. To see if we can obtain a much better model, we need to run our grid search for a longer period of time that way more models can be trained.
We will check the MAE:
# Compare the MAE of the default and tuned XGBoost
h2o.mae(valid_def_xgb_perf)
h2o.mae(valid_tuned_xgb_perf)
Output:
0.3108205
0.2989957
In the case of an interest rate decision, an MAE of 0.30 is good enough as it tells us that, on average, the model would predict a very close interest rate to what someone with "x" characteristics should get. However, for some use cases the MAE of 0.30 might be too high, so it all depends on the application to decide whether or not our MAE results are satisfactory. We will see if the Deep Learning model can yield a lower RMSE and MAE.
For our grid search in Flow, we will try to explore a few more parameters that could potentially help the scores of our model. We will try to find good values for L1 and L2 regularizations, we will explore some values for the learning rate, also the distribution and booster. Please see the definitions below:
1. reg_alpha: Specify a value for L1 regularization. L1 regularization encourages sparsity, meaning it will make the weights at the leaves become 0. This value defaults to 0.
2. reg_lambda: Specify a value for L2 regularization. L2 Regularization makes some of the weights at the leaves to be small, but not zero. This defaults to 1.
3. learn_rate (alias: eta): Specify the learning rate by which to shrink the feature weights. Shrinking feature weights after each boosting step makes the boosting process more conservative and prevents overfitting. The range is 0.0 to 1.0. This value defaults to 0.3.
4. distribution: Specify the distribution (i.e., the loss function). The options are AUTO, Bernoulli, multinomial, gaussian, poisson, gamma, or tweedie. Since our response is numeric, we will just include poisson, Tweedie, Gaussian, and gamma.
5. booster: Specify the booster type. This can be one of the following: "gbtree," "gblinear," or "dart." Note that "gbtree" and "dart" use a tree-based model while "gblinear" uses a linear function. This value defaults to "gbtree."
Start by building an XGBoost model the same way we did in Task 4. Find the training set (the frame with 350k rows and 27 columns), assign a model id such flow-xgb-grid so that it is easy to find the models later on; for now, you can set nfolds to 3. Choose ORIGINAL_INTEREST_RATE for the response_column, select the same eight columns as before to be ignored.
FIRST_PAYMENT_DATE,MATURITY_DATE,MORTGAGE_INSURANCE_PERCENTAGE,PREPAYMENT_PENALTY_MORTGAGE_FLAG,PRODUCT_TYPE,LOAN_SEQUENCE_NUMBER,PREPAID,DELINQUENT
You can set the seed to 42 and since we are doing a different grid search with more parameters, set ntrees to 100, and max_depth to 9, this should help us train a few more models as opposed of using more trees. Now, check the "Grid?" box next to the explanation of learn_rate. Then, add the following list of values into the aforementioned parameters 0.24; 0.26; 0.28; 0.30; 0.33; 0.36;
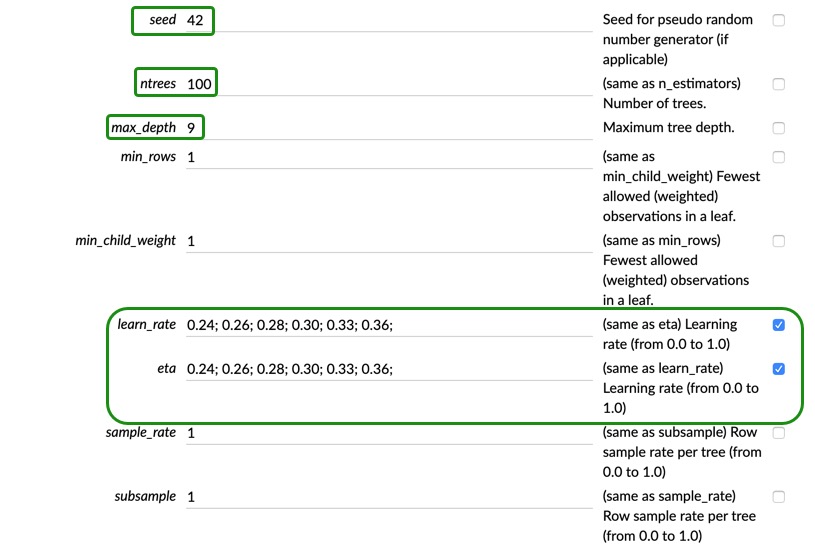
Scroll down to the early stopping section, and make sure your settings look similar to ours.

Keep scrolling down to distribution and check the box next to it, again. Now you should be able to select the distributions that you want. Select "gaussian," "gamma," and "tweedie"

Scroll down to the Expert settings, and check the "Grid?" box for booster type and select all three. Lastly, click the "Grid?" box for reg_lambda and reg_alpha and add the following list 0.3;0.4;0.5;0.6;0.7;0.8;0.9; and 0.1;0.2;0.35;0.5;0.6; respectively.

Before clicking "Build Model" update the "GRID SETTINGS" to the settings shown below:

When you are done, click on Build Model and wait for it to finish. We are just letting this grid run for 10 minutes; Once it is done, click on View, and you should be able to see the following models:
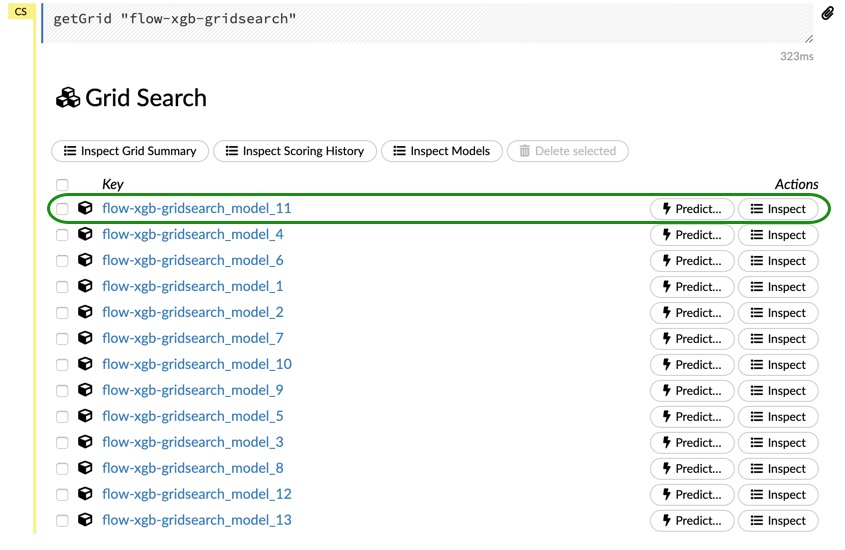
Go ahead and click on the first model. Inspect the results on your own, look for the parameters that were used for the best model, compare the results from flow cross-validation to the results we obtained in the last grid search that we did in the Jupyter Notebook. How do the results compare? How are they different? Did you get the results you were expecting?
We will try to tune our Deep Learning model and see if we can improve the scores from the default model.
Two of the most important parameters of a Deep Learning model are the number of neurons in the hidden layers and the number of epochs. The parameter for both hidden neurons and layers is "hidden", and we can specify the hidden layer sizes. For example, to define a two-hidden-layer model, with 200 neurons in each layer, we would define it as [200, 200]. If you wanted to have three hidden layers with 300 neurons in the first layer, 200 in the second one, and 100 in the third one, we would do it as follows [300, 200, 100]. The epochs allows us to specify the number of times to iterate (stream) the dataset, and this value can be a fraction. We will try to find a good size for our hidden layer, and we will take care of the number of epochs with early stopping.
Since there are so many combinations for the size of hidden layers, the easiest thing to do is to just do a random search and use one of the models that you find. In this self-paced course, we will try to find a good size for the hidden layer taking into consideration the time it takes to train, and then we will try to tune that model. We will explore models with up to two hidden layers for you to see, but for the purpose of this self-paced course, we will not try to tune more complex DL models.
With the code shown below, you can do a random search to explore several sizes of hidden layers. The way we chose the number of neurons is selecting multiples of 165, which is the size of our input layer (although we do not have 165 predictors, we have predictors that have multiple categories, and they all add up to 165, and thus the number of neurons) and we also added two random sizes, 100 and 200, just to see how they perform.
For the activation function, we could use the rectifier activation function, as it is one of the best amongst the three activation functions in H2O-3. We could also try the maxout activation function, but the model usually takes much longer to train. Since H2O-3 gives us the option to add dropout ratios to our activation functions, we will use the rectifier_with_dropout activation function. Therefore, we need to find a good dropout rate for our hidden layer.
hidden_dropout_ratios improves generalization, which could help our model perform better. The range is >= 0 to , and the default is 0.5.
dl = H2ODeepLearningEstimator(seed = 42,
model_id = 'DL',
nfolds = 0,
keep_cross_validation_predictions = False,
epochs = 10,
activation = 'rectifier_with_dropout',
stopping_rounds = 5, #default
stopping_tolerance = 1e-3, #default
stopping_metric = "rmse") #default
hyper_params = {'hidden' : [[100, 100], [165, 165], [200,200], [330,330],
[165, 200]],
'hidden_dropout_ratios' : [[0,0], [0.01,0.01], [0.15,0.15],
[0.30, 0.30],[0.5,0.5]]}
search_criteria_tune = {'strategy': "RandomDiscrete",
'max_runtime_secs': 900, #15 min
'max_models': 100, ## build no more than 100 models
'seed' : 42}
dl_grid = H2OGridSearch(model = dl,
hyper_params = hyper_params,
grid_id = 'random_dl_grid',
search_criteria = search_criteria_tune)
%time dl_grid.train(x = x, y = y, training_frame = train, validation_frame = valid)
Print the results from the grid search:
hidden_per = dl_grid.get_grid(sort_by = 'rmse', decreasing = False)
hidden_per.sorted_metric_table()
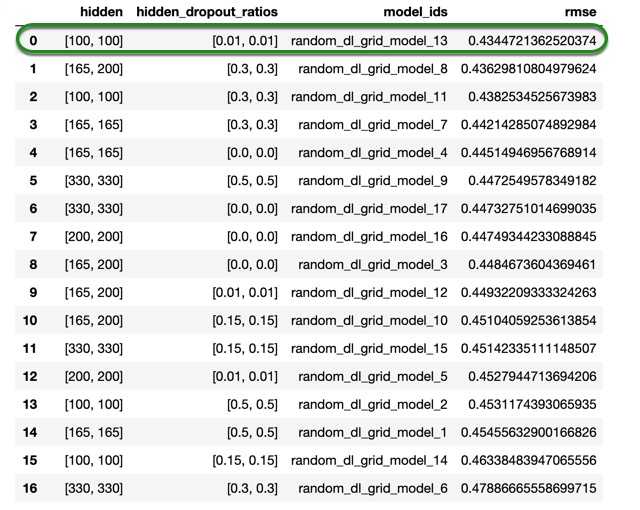
Note: your grid search results for the Deep Learning model might be different to ours, that is because the deep learning models are hard to reproduce. Although, if you use the values that we find, you should get similar results at the end. With that being said, you can use the values that we provide in the self-paced course, or you could use the values that you get from your own grid search and compare the results at the end.
From the results above, we can see that our simplest DL model has the best performance with almost no dropout, as the model with the best score has a hidden_dropout_ratios of 0.01. so for the next grid search, we will use that value.
Another parameter that is important in deep learning models is the learning rate. H2O-3 offers a parameter called adaptive_rate(ADADELTA) and is enabled by default. Enabling the adaptive learning rate is roughly equivalent to turning on momentum training (as each model coefficient keeps track of its history), it is only slightly more computationally expensive (it uses an approximate square-root function that only costs a few clock cycles). Also, different hyper-parameters for adaptive learning rate can affect the training speed (at least for Rectifier activation functions, where back-propagation depends on the activation values).
For cases where fastest model training is required (possibly at the expense of highest achievable accuracy), manual learning rates without momentum can be a good option, but in general, adaptive learning rate simplifies the usage of H2O Deep Learning and makes this tool highly usable by non-experts, for that reason, we won't try to tune that parameter, or the parameters related to the learning rate.
We will update the parameters with the values we just found and we will do a quick exploration for l2 and max_w2
1. l2: Specifies the L2 regularization to add stability and improve generalization; sets the value of many weights to smaller values. This value defaults to 0.
2. max_w2: Specifies the constraint for the squared sum of the incoming weights per unit. This value defaults to 3.4028235e38
Note: The values for l2 have been chosen based on previous experience and the values for max_w2 were chosen based on the default value.
The grid search is as follow:
dl = H2ODeepLearningEstimator(epochs = 10,
hidden = [100,100],
hidden_dropout_ratios = [0.01,0.01],
seed = 42,
model_id = 'DL',
activation = 'rectifier_with_dropout',
stopping_rounds = 3,
stopping_tolerance = 1e-3, #default
stopping_metric = "rmse", #default
adaptive_rate = True)
hyper_params = {'max_w2' : [1e38, 1e35, 1e36, 1e37, 1e34, 5e35],
'l2' : [1e-7, 1e-6, 1e-5, 1e-4, 5e-4, 1e-3, 0],
}
search_criteria_tune = {'strategy': "RandomDiscrete",
'max_runtime_secs': 900, #15 min
'max_models': 100, ## build no more than 100 models
'seed' : 42
}
dl_grid = H2OGridSearch(model = dl,
hyper_params = hyper_params,
grid_id = 'random_dl_search',
search_criteria = search_criteria_tune)
%time dl_grid.train(x = x, y = y, training_frame = train, validation_frame = valid)
Retrieving the results:
dl_perf = dl_grid.get_grid(sort_by = 'rmse', decreasing = False)
dl_perf.sorted_metric_table()
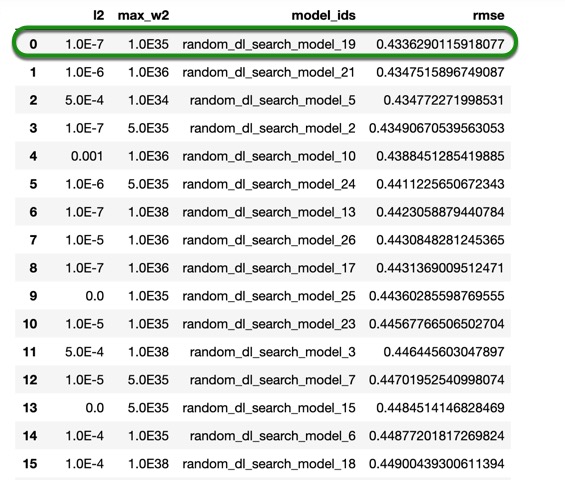
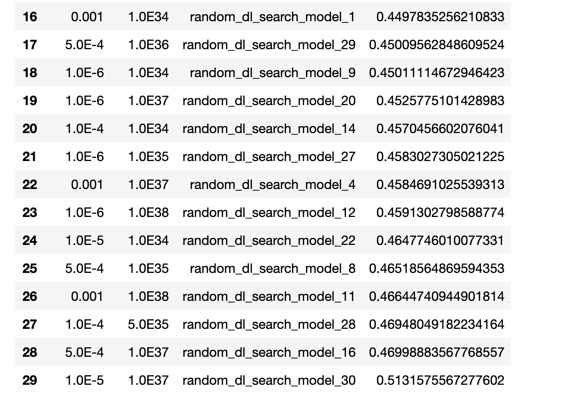
As we can see, the RMSE value slightly improved with the grid search that we just did, compared to the first grid search. Although, when we compare it to the default model, our tuned model has improved, yielding a better score. If you recall, at the beginning of the self-paced course, we mentioned that H2O's DNN model allows you to do checkpointing. The checkpoint option allows you to specify a model key associated with a previously trained model. This will build a new model as a continuation of a previously generated model. Since we were training our model with only 10 epochs, let's now train the same model with 200 epochs while using early stopping to see if we get better results. Also, set reproducible=True, this model will take longer to train, but it will yield similar results when you re-run it.
To be able to use checkpointing, we need to retrieve the model from the grid search that we just did, and then use the model id to continue training the same model. There are several parameters that can not be changed, and for that reason, we need to specify them one more time; however, this guarantees us that we are training the same model from the grid search. To learn more about checkpointing, please check the Documentation section on Checkpoint
Note: the following model will only be generated if your best model from the previous grid has the same parameters as ours. If you obtained different parameters, make sure you update them before running the following line of code.
best_dl_model = dl_grid.models[0]
dl_checkpoint = H2ODeepLearningEstimator(checkpoint = best_dl_model.model_id,
epochs = 200,
hidden = [100,100],
hidden_dropout_ratios = [0.01,0.01],
adaptive_rate = True,
l2 = 1.0e-7,
max_w2 = 1e35,
reproducible = True,
model_id = 'DL_checkpoint',
activation = 'rectifier_with_dropout',
distribution = 'auto',
seed = 42,
stopping_metric = 'RMSE',
stopping_tolerance = 1e-3,
stopping_rounds = 5)
%time dl_checkpoint.train(x = x, y = y, training_frame = train, validation_frame = valid)
Note: we must specify the parameters that we tuned, because if we don't, H2O-3 will set those parameters to their default values, and most of the parameters that we tuned can not be changed when we use checkpoint.
Print the model summary by typing the name of your model in a new cell and running it, as shown in the image below.
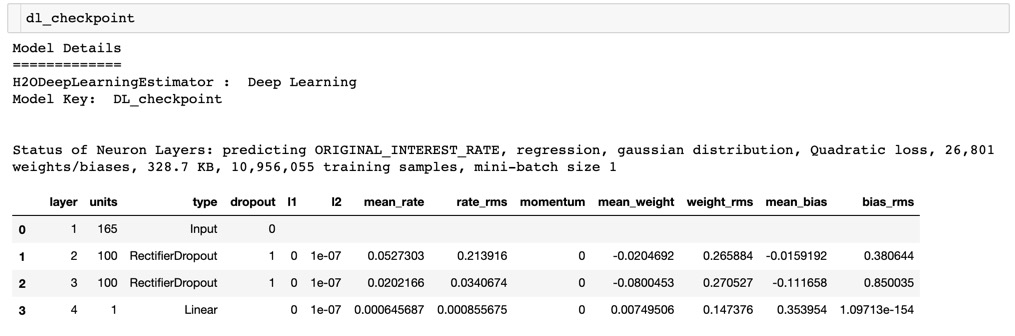

As you can see in the image above, the RMSE and MAE improved, meaning that by increasing the number of epochs, we were able to improve the performance of our model.
You can also tune a Deep Learning model in Flow, and you would do it in the same way we did with the XGBoost. Give it a try on your own, using the parameters that we found, do a local search with them. For example, since we found the hidden_dropout_ratios to be 0.01, you could do a grid search where you use the values 0.010; 0.05; 0.015; 0.3 Try to do the same with some of the other parameters that we found and see if you can get better results. Once you are done with Flow, go back to your Jupyter Notebook.
Let's see how our default model performance compares to the tuned one.
tuned_dl_per = dl_checkpoint.model_performance(valid)
print("Default DL Model RMSE: %.4f \nTuned DL Model RMSE:%.4f" % (default_dl_per.rmse(), tuned_dl_per.rmse()))
Output:
Default DL Model RMSE: 0.4673
Tuned DL Model RMSE:0.4144
Now print the MAE of both models
print("Default DL Model MAE: %.4f \nTuned DL Model MAE:%.4f" % (default_dl_per.mae(), tuned_dl_per.mae()))
Output:
Default DL Model MAE: 0.3292
Tuned DL Model MAE:0.3012
Both scores improved with the grid searches that we did. In fact, our deep learning model had the greatest improvement out of the two models we tuned; however, the XGBoost still performed slightly better than the Deep Learning model.
We will now see how our models perform on the test set.
Deep Dive
We will try to tune our Deep Learning model and see if we can improve the scores from the default model.
Two of the most important parameters of a Deep Learning model are the number of neurons in the hidden layers and the number of epochs. The parameter for both hidden neurons and layers is "hidden", and we can specify the hidden layer sizes. For example, to define a two-hidden-layer model, with 200 neurons in each layer, we would define it as [200, 200]. If you wanted to have three hidden layers with 300 neurons in the first layer, 200 in the second one, and 100 in the third one, we would do it as follows [300, 200, 100]. The epochs allows us to specify the number of times to iterate (stream) the dataset, and this value can be a fraction. We will try to find a good size for our hidden layer, and we will take care of the number of epochs with early stopping.
Since there are so many combinations for the size of hidden layers, the easiest thing to do is to just do a random search and use one of the models that you find. In this self-paced course, we will try to find a good size for the hidden layer taking into consideration the time it takes to train, and then we will try to tune that model. We will explore models with up to two hidden layers for you to see, but for the purpose of this self-paced course, we will not try to tune more complex DL models.
With the code shown below, you can do a random search to explore several sizes of hidden layers. The way we chose the number of neurons is selecting multiples of 165, which is the size of our input layer (although we do not have 165 predictors, we have predictors that have multiple categories, and they all add up to 165, and thus the number of neurons) and we also added two random sizes, 100 and 200, just to see how they perform.
For the activation function, we could use the rectifier activation function, as it is one of the best amongst the three activation functions in H2O-3. We could also try the maxout activation function, but the model usually takes much longer to train. Since H2O-3 gives us the option to add dropout ratios to our activation functions, we will use the rectifier_with_dropout activation function. Therefore, we need to find a good dropout rate for our hidden layer.
hidden_dropout_ratios improves generalization, which could help our model perform better. The range is >= 0 to , and the default is 0.5.
# Do a Grid Search to tune the hidden layers and the droput ratio
dl_hidden_grid <- h2o.grid(algorithm = "deeplearning",
grid_id = "dl_hidden_grid",
activation = "RectifierWithDropout",
epochs = 10,
seed = 42,
stopping_rounds = 3,
stopping_metric ="RMSE",
stopping_tolerance = 1e-3,
x = x,
y = y,
training_frame = train,
validation_frame = valid,
hyper_params = list(
hidden = list(c(100, 100), c(165, 165), c(200, 200), c(330, 330),
c(165, 200)),
hidden_dropout_ratios = list(c(0,0), c(0.01,0.01), c(0.15,0.15),
c(0.30, 0.30), c(0.5,0.5))),
search_criteria = list(
strategy = "RandomDiscrete",
max_runtime_secs = 900,
seed = 42))
Print the results from the grid search:
# Retrieve the Grid Search
dl_hidden_grid_rmse <- h2o.getGrid(grid_id = "dl_hidden_grid", sort_by = "rmse", decreasing = FALSE)
as.data.frame(dl_hidden_grid_rmse@summary_table)
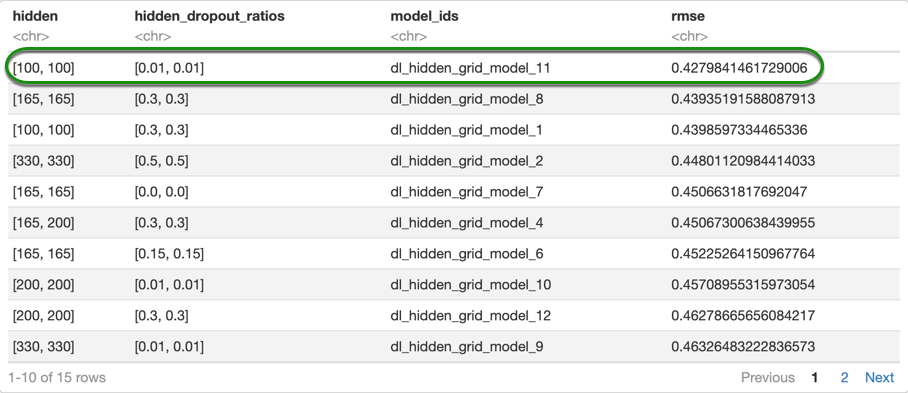
Note: your grid search results for the Deep Learning model might be different to ours, that is because the deep learning models are hard to reproduce. Although, if you use the values that we find, you should get similar results at the end. With that being said, you can use the values that we provide in the self-paced course, or you could use the values that you get from your own grid search and compare the results at the end.
From the results above, we can see that our simplest DL model has the best performance with almost no dropout, as the model with the best score has a hidden_dropout_ratios of 0.01. so for the next grid search, we will use that value.
Another parameter that is important in deep learning models is the learning rate. H2O-3 offers a parameter called adaptive_rate(ADADELTA) and is enabled by default. Enabling the adaptive learning rate is roughly equivalent to turning on momentum training (as each model coefficient keeps track of its history), it is only slightly more computationally expensive (it uses an approximate square-root function that only costs a few clock cycles). Also, different hyper-parameters for adaptive learning rate can affect the training speed (at least for Rectifier activation functions, where back-propagation depends on the activation values).
For cases where fastest model training is required (possibly at the expense of highest achievable accuracy), manual learning rates without momentum can be a good option, but in general, adaptive learning rate simplifies the usage of H2O Deep Learning and makes this tool highly usable by non-experts, for that reason, we won't try to tune that parameter, or the parameters related to the learning rate.
We will update the parameters with the values we just found and we will do a quick exploration for l2 and max_w2
1. l2: Specifies the L2 regularization to add stability and improve generalization; sets the value of many weights to smaller values. This value defaults to 0.
2. max_w2: Specifies the constraint for the squared sum of the incoming weights per unit. This value defaults to 3.4028235e38
Note: The values for l2 have been chosen based on previous experience and the values for max_w2 were chosen based on the default value.
Before we move on to the next grid search, we need to retrieve the best model from our previous grid search because we will use the two parameters that we tuned:
top_dl <- h2o.getModel(dl_hidden_grid_rmse@model_ids[[1]]) #getting the best model
The grid search is as follow:
# Grid Search to tune the Max W2 and L2
dl_random_grid_rmse <- h2o.grid(algorithm = "deeplearning",
grid_id = "dl_random_grid",
activation = "RectifierWithDropout",
hidden = top_dl@allparameters[["hidden"]],
epochs = 10,
seed = 42,
hidden_dropout_ratios = top_dl@allparameters[["hidden_dropout_ratios"]],
stopping_rounds = 3,
stopping_metric = "RMSE",
stopping_tolerance = 1e-3,
x = x,
y = y,
training_frame = train,
validation_frame = valid,
hyper_params = list(
max_w2 = c(1e38, 1e35, 1e36, 1e37, 1e34, 5e35),
l2 = c(1e-7, 1e-6, 1e-5, 1e-4, 5e-4, 1e-3, 0)),
search_criteria = list(
strategy = "RandomDiscrete",
max_runtime_secs = 900,
seed = 42))
Retrieving the results:
# Retrieve the Grid Search
dl_random_grid_rmse <- h2o.getGrid(grid_id = "dl_random_grid", sort_by = "rmse", decreasing = FALSE)
as.data.frame(dl_random_grid_rmse@summary_table)
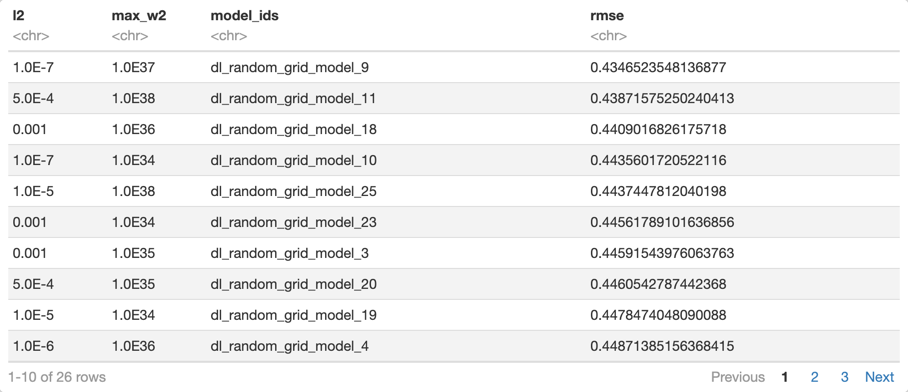
As we can see, the RMSE value didn't improve with the grid search that we just did, compared to the first grid search. Although, by setting a different value for L2 and Max W2, we can increase the stability of our model, and it can also help with generalization. If you recall, at the beginning of the self-paced course, we mentioned that H2O's DNN model allows you to do checkpointing. The checkpoint option allows you to specify a model key associated with a previously trained model. This will build a new model as a continuation of a previously generated model. Since we were training our model with only 10 epochs, let's now train the same model with 400 epochs while using early stopping to see if we get better results. Also, set reproducible=True, this model will take longer to train, but it will yield similar results when you re-run it.
To be able to use checkpointing, we need to retrieve the model from the grid search that we just did, and then use the model id to continue training the same model. There are several parameters that can not be changed, and for that reason, we need to specify them one more time; however, this guarantees us that we are training the same model from the grid search. To learn more about checkpointing, please check the Documentation section on Checkpoint
Note: the following model will only be generated if your best model from the previous grid has the same parameters as ours. If you obtained different parameters, make sure you update them before running the following line of code.
Again, we need to retrieve the best model from our previous grid search to access the values that we tuned with out previous grid searches:
# Retrieve the best model from the Grid Search
tuned_dl <- h2o.getModel(dl_random_grid_rmse@model_ids[[1]]) #getting the best model
# Checkpointing for DL model to increase the number of epochs
dl_checkpoint <- h2o.deeplearning(x = x,
y = y,
training_frame = train,
model_id = "dl_checkpoint",
validation_frame = valid,
checkpoint = dl_random_grid_rmse@model_ids[[1]],
activation = "RectifierWithDropout",
hidden = tuned_dl@allparameters[["hidden"]],
epochs = 400,
seed = 42,
hidden_dropout_ratios = tuned_dl@allparameters[["hidden_dropout_ratios"]],
l2 = tuned_dl@parameters$l2,
max_w2 = tuned_dl@parameters$max_w2,
reproducible = TRUE,
stopping_rounds = 5,
stopping_metric = "RMSE",
stopping_tolerance= 1e-5)
Note: we must specify the parameters that we tuned, because if we don't, H2O-3 will set those parameters to their default values, and most of the parameters that we tuned can not be changed when we use checkpoint.
Print the model summary by typing the name of your model in a new cell and running it, as shown in the image below.
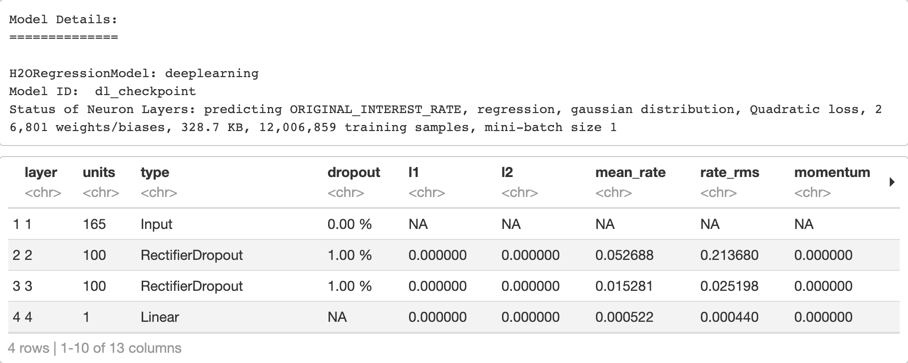

As you can see in the image above, the RMSE and MAE improved, meaning that by using the checkpointing and increasing the number of epochs, we were able to improve the performance of our model.
If you wanted to do this in Flow, you could do it in the same way we did with the XGBoost. Give it a try on your own, using the parameters that we found, do a local search with them. For example, since we found the hidden_dropout_ratios to be 0.01, you could do a grid search where you use the values 0.010; 0.05; 0.015; 0.3.
Let's see how our default model performance compares to the tuned one.
# Save the validation performance of the best DL model
valid_tuned_dl_perf <- h2o.performance(dl_checkpoint, valid)tuned_dl_per.rmse()))
# Compare the RMSE of the default and tuned DL model
h2o.rmse(valid_def_dl_perf)
Output:
0.4434367
# Print the validation RMSE for the tuned model
h2o.rmse(valid_tuned_dl_perf)
Output
0.4147817
Now print the MAE of both models
# Compare the MAE of the default and tuned DL model
h2o.mae(valid_def_dl_perf)
# Tuned model MAE
h2o.mae(valid_tuned_dl_perf)
Output:
0.3277302
0.2993333
As we can see, both scores improved with the grid searches that we did. In fact, our deep learning model had the greatest improvement out of the two models we tuned; however, the XGBoost still performed slightly better than the Deep Learning model.
We will now see how our models perform on the test set.
Deep Dive
Now that we have done some tuning for our models, we will see how the models would perform on unseen data. Let's first print the final RMSE for both models. To do so, we need to evaluate the performance of our models on the test set.
dl_test_per = dl_checkpoint.model_performance(test)
xgb_test_per = best_xgb_model.model_performance(test)
Print the RMSE for both models:
print("XGBoost Test RMSE: %.4f \nDeep Learning Model Test RMSE: %.4f " %
(xgb_test_per.rmse(), dl_test_per.rmse()))
Output:
XGBoost Test RMSE: 0.4139
Deep Learning Model Test RMSE: 0.4176
The test RMSE for both models is very close to the validation results, which means that our validation set cross-validation approach worked well. As we mentioned before, the RMSE score adds more penalty to larger errors. But based on the RMSE, on average, the tuned models' predictions on the test set are about 0.41 off.
Now, let's look at the MAE score:
print("XGBoost Test MAE: %.4f \nDeep Learning model Test MAE: %.4f " %
(xgb_test_per.mae(), dl_test_per.mae()))
Output:
XGBoost Test MAE: 0.2993
Deep Learning model Test MAE: 0.3025
If we do not take into consideration the penalty that the RMSE adds, and focus on the MAE to evaluate our models, we see that the predictions of the interest rate are 0.3 off from the actual values, which is a good indication that the model is making good predictions for the interest rate. Let's see some of the predictions for both models.
We will take a look at the first ten predictions of both models, compared to the actual interest value.
gb_tuned_pred = best_xgb_model.predict(test) #get predictions from xgboost
test_rate_pred = test['ORIGINAL_INTEREST_RATE'].cbind(xgb_tuned_pred)#combined xgb predictions with actual interest rate
dl_tuned_pred = dl_checkpoint.predict(test)#get predictions from Deep Learning Model
test_rate_pred.cbind(dl_tuned_pred)
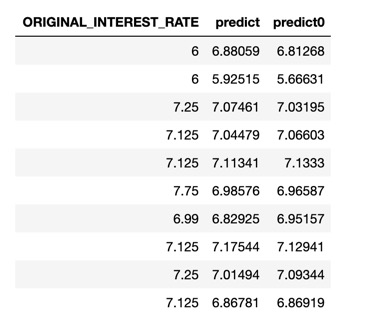
Please note that the predict column has the predictions for the XGBoost model, and the predict0 column has the predictions for the Deep Learning model. As we can see in the image above, both predictions are close to the actual values. Although there might be some predictions that might be very off, the RMSE and MAE proved to us that both models make good predictions.
Note: You will not get the exact same results for the Deep Learning model. The values shown in this self-paced course for that model are the final values that we obtained, and they should only be a reference for you. You should expect values similar to ours, but not the same.
If you do not want to attempt the challenge in the next task, feel free to shut down your cluster, or you can shut it down after you attempt the challenge.
Now that we have done some tuning for our models, we will see how the models would perform on unseen data. Let's first print the final RMSE for both models. To do so, we need to evaluate the performance of our models on the test set.
# Save the test performance of the tuned models
tuned_xgb_test_perf <- h2o.performance(tuned_xgb, test)
tuned_dl_test_perf <- h2o.performance(dl_checkpoint, test)
Print the RMSE for both models:
# Print the test RMSE of the XGB and DL model
h2o.rmse(tuned_xgb_test_perf)
h2o.rmse(tuned_dl_test_perf)
Output:
0.4138809
0.4170765
The test RMSE for both models is very close to the validation results, which means that our validation set cross-validation approach worked well. As we mentioned before, the RMSE score adds more penalty to larger errors. But based on the RMSE, on average, the tuned models' predictions on the test set are about 0.41 off.
Now, let's look at the MAE score:
# Print the test MAE of the XGB and DL model
h2o.mae(tuned_xgb_test_perf)
h2o.mae(tuned_dl_test_perf)
Output:
0.2996863
0.3000834
If we do not take into consideration the penalty that the RMSE adds, and focus on the MAE to evaluate our models, we see that the predictions of the interest rate are 0.3 off from the actual values, which is a good indication that the model is making good predictions for the interest rate. Let's see some of the predictions for both models.
We will take a look at the first ten predictions of both models, compared to the actual interest value.
# Make predictions with the XGB and DL model
tuned_xgb_pred <- h2o.predict(tuned_xgb, test)
tuned_dl_pred <- h2o.predict(dl_checkpoint, test)
# Compare the predictions from XGB, and DL models with the original reponse
h2o.cbind(test[, c("ORIGINAL_INTEREST_RATE")], tuned_xgb_pred, tuned_dl_pred)
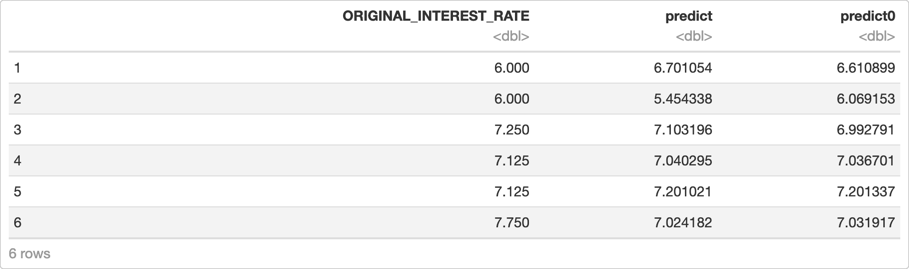
Please note that the predict column has the predictions for the XGBoost model, and the predict0 column has the predictions for the Deep Learning model. As we can see in the image above, both predictions are close to the actual values. Although there might be some predictions that might be very off, the RMSE and MAE proved to us that both models make good predictions.
Note: You will not get the exact same results for the Deep Learning model. The values shown in this self-paced course for that model are the final values that we obtained, and they should only be a reference for you. You should expect values similar to ours, but not the same.
If you do not want to attempt the challenge in the next task, feel free to shut down your cluster, or you can shut it down after you attempt the challenge.
h2o.shutdown()
We tuned the Deep Learning model with two hidden layers with 100 neurons in each layer. Try to tune a Deep Learning model on your own with two layers, or more, and with the number of neurons that you want. You can follow the same procedures as before, but if you wanted to have models wiht three hidden layers you will have to use something like [165,165, 165], and for some parameters such as the dropout ratios, you will need to also have two values, such as [0.01, 0.01, 0.01], and so on. If you attempt the challenge, you can download your Notebook with your work, and just restart the lab; that way, you have at least 2 hours to tune the new model. Once you're done with the self-paced course, shut down your cluster, or end the lab.
Please make sure you check out our H2O AutoML Self-Paced Course - Introduction to Machine Learning with H2O-3 - AutoML